| 梦远书城 > 类书 > 图书集成乾象典 | 上页 下页 |
| 日月部汇考一(3) |
|
|
|
明,罗雅谷《交食历指》 《界说》 凡物体能隔他物之象,使不至目,则为“暗体。”若以体之一面受光,而光复透射出于彼面,则为“彻体。”〈如玻璃水精是也〉○目所司存,惟光惟色,而色又随光发见,故解“彻体”,必以通光,解“暗体”,必以其能隔他象。如月掩日而日全食,昼为之晦,恒星皆见。尔时太阳在外,体质明显,又坚密无比,光力甚厚,乃为月体所隔,不能映见微光可证。月乃全非彻体,而全为暗体○。彻体有二,通明之极,全无隔碍者为甚彻;虽则透光,而微杂昏蒙者为“次彻。” 光在本体为原光,其出而显他物之象为照光○。日有原光,地与月皆借之为光者,照光也。谓显他物之象者,因他物之势随施随受,有原先后,无时先后也。 非如寒热燥湿之类,渐及于物,力尽而止。 《原光》以直径发照为最光,因而旁及者为次光○。日光正照以直线至于物体,则为最光。有物隔之,旁周映射,则生次光。如云之上,日体所照,最光也。云之下,不复见日,而犹有光,是次光也。 满光者,原光之全体所发。少光者,原光之半体所发○。日未全出地,平上所生光为少光。全升在上,则生满光。日食时未全食,则存少光。既以复圆,即得满光。 景之四周有最光绕之,即景为次光○。以景为明者,误也;以影为暗者,亦误也。称景为明暗之中,庶几近之,盖全无光乃为暗。今至夜子初,人在地景至深之中,去最光极远,而近目之物尚能别识,即见景中犹存微光,不失为“次光”也。 最光所不及为“初景”,次光所不及,则为“次景○。”景与光并行,光渐微,景渐厚,故“次景”与“最光”相反。若初景,即次光也。 最光全不及之处,则为“满景。”若受正照之微光,即为“缺景○。”景与光正相反,无景之极则为“满光”,无光之极则为“满景”。 光景图 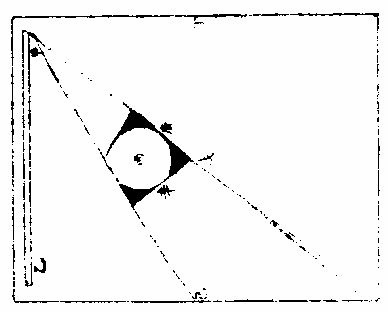 光景图说 假如甲乙为施光之物,丙为暗球,从甲出正照之光过丙球左右,其切丙之界者,得甲戊及甲己,从乙出光,又得乙戊及乙丁。其庚戊辛为最光,全不及之处则满景也。若庚戊辛戊以外,则甲乙光体之多分,渐照之至乙丁甲己乃全光之界,即自戊至丁至己,丙球之景渐薄以趋于尽矣。 《太阳光照月及地》 日月地三,球体大小不等。地为静体,日月则有诸种,行度则有高庳内外。其去地去人远近不等。法当以大小之比例及其相远相近之比例,推其施光受光之体势,乃得景之体势,因而得交食之体势。盖交食者生于景,景生于光,不寻其本而求其末,无法可得。 其说五章。 明暗两体相等图  《明暗两体相等图说》。 一曰:有两球于此,一为暗体,一为明体,而小大等,即明者以半面施光,暗者以半面受光○。如图甲为明球,乙为暗球,小大等,即其径丙丁及戊己各与甲乙线为直角,而丙丁与戊己等,即甲丙甲丁,乙戊乙己与甲庚乙辛,皆以半径相等,而丙庚丁半球,与戊辛己半球亦相等。今于明球之旁,从丙从丁出两切线,至暗球之旁戊己,戊己与丙丁为并行线,即丙戊与丁己亦并行线也。又因丙戊乙及丁己乙俱为直角,即戊丙甲及己丁甲亦俱直角,即丙戊丁己线不能割两球,而止切两周于丙于戊、于丁于己,其所抱为丙庚丁、为戊辛己,是甲乙两球之各半也。若日月地三球相等,而月与地皆以半面受太阳之光,如上所说,则定朔日食,半地面宜皆见之,安得复有南北不等食分?望日,太阴全食时,才食既即生光,安得复有食甚时刻及既内分?今皆不然,可见三球无相等之球。 明体大暗体小图 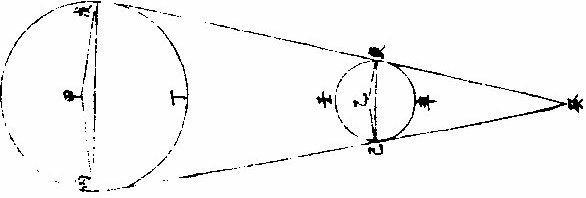 “明体大、暗体小”《图》说。 二曰明体大,暗体小,则施光以小半,受光以大半○。 如图甲为明球,乙为暗球,作两切线,为丙己,为戊庚,从四切点作横线,为丙戊,为己庚。甲既大球,即己丙戊为锐角,丙己庚角为钝角。如曰不然,或皆为直角,即庚戊丙戊庚己亦皆直角,两切线必平行,而乙球与甲球等,必不然也。或己丙戊反为钝角,而丙己庚反为锐角,即两切线不能相交于癸,又不然也。今以两切线相交于癸,明己丙戊为锐角,丙己庚为钝角。 即于丙丁戊弧内作负圈角,必钝角矣;于己壬庚内作负圈角,必锐角矣。故丙丁戊施光者不及半圈,己壬庚受光者又不止半圈也。因此推知太阳照地,及太阴必各照其大半,而暗体所隔之日光渐远,又渐敛渐进以趋于一处,即景居暗球之背,不得不为角体之形矣。又因此推求望日先后,人目所见,太阴受日之光不长不消者,久之而后生魄。此为何故?盖亦因月体以大半受光,小半入于人目,光不辄转,而魄未遽见,故未望时已见全光,已望后犹未失全光也 明体小暗体大图  “明体小、暗体大”《图》说。 三曰:“明体小,暗体大,则施光以大半,受光以小半○”,如前《图》反论之,可明太阴何以照地?而地何反隔日之光也? 大施小受图 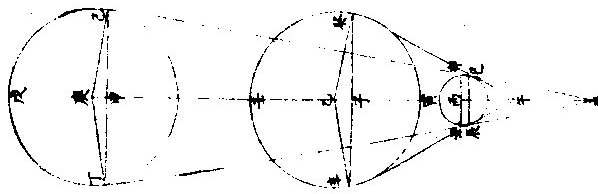 大施小受图说 四曰“大施”、“小受。”愈相近,则施者之小半愈小,受者之大半愈大○。如图丙为小暗球,甲与乙皆大明球,作庚未直线,过三球心,以交于左右切线。其乙球之两切线交于午,甲球之两切线交于未,即庚未长于乙午,而庚丁未与乙辛午两角,庚丁与乙辛两线皆相等,则庚未线与庚丁线之比例,大于乙午与乙辛,而丁“庚未角大于辛乙午角也。又庚未线过三球之心,必截丁己辛癸两线为两平分,而庚甲丁乙子辛两形内之甲与子皆为直角”,则其余庚丁两角并乙辛两角并,皆等一直角,即两并率等两并率之甲庚丁角大于子乙辛角,各减之,所存庚丁甲角,必小于乙辛子角矣。次以庚丁甲及乙辛子不等“之两角,各减庚丁未及乙辛午相等之两直角,所存甲丁未角,更大于子辛午角,又《丁戊己弧》内作负圈角,必等于甲丁未角,《辛壬癸弧》内作负圈角,必等于子辛午角,《辛壬癸弧》之负圈角,既小于丁戊己弧之负圈角,则《辛壬癸弧》必大于丁戊己弧。 夫辰寅巳与辛壬癸相似之弧也,丑寅卯与丁戊己”,亦相似之弧也。〈大小圈左右各有切线其切点过分圈之线其所分大小圈分各相似其大小两弧亦相似〉即辰寅巳弧亦大于丑寅卯弧,可见明球在近比在远者,尤能照小暗球之多分也○。因此推知日全食而视为大者,日体去月体远故也。日全食而视为小者,日体去月体近故也。何以分远近?日与月俱有自行圈,与地不同心,其行于自行圈之上下为最高最庳,则为距地之远近,因生景之大小也。日既全食矣,又何以分大小?月掩日至,既有时昼晦,恒星皆见,虫飞鸟栖,此为全食。而大月在日内,从中掩蔽,虽至食既,而其四周日光皆见,历家谓之“金环”,此为全食而小矣。若然者,日与月与地,相去或远或近之所繇生也。 小施大受图  小施大受图说 五曰“小施。”大受。愈相远,则施者之大半加小,受者之小半渐大○。如图甲乙皆为小明球,丙为大暗球,乙去丙远,于甲作各切线,过三球心之直线,皆如前。次从暗球心丙至各切点,作丙丁、丙己、丙庚、丙辛各半径,得丙丁为丁壬之垂线,丙庚为庚癸之垂线,而丁与庚皆为直角,丙丁与丙庚两线又等,则丙癸线与丙庚半径之比例,大于丙壬与丙丁,而丙庚癸角又大于丙丁壬角也。依显丙辛癸角亦大于丙己壬角以并前率为庚丙辛合角,亦大于丁丙己合角,而其弧庚戊辛必大于丁戊己。可见小明球照大暗球,愈远愈照其多分也。 今依本图,设丙为地外切线。〈癸辛也〉以内为《地景》。〈日光过丙大球所出景〉甲、乙两小球为月体。其两小球之小大既等,则同以外切线为外光之界,或为内景之界。惟因月体循本轮行,时居上周如乙,则去地远;时居下周如甲,则去地近。以是月食之分数有多有寡。月居影厚处,如甲左右,则食多;月居影薄处,如乙左右,则食寡。故曰:“月食有多寡”者,亦相距或远或近之所由生也。 景之处所 凡光以直线照物,体其无光之处,则有景之处也。欲于交食时求影所在,理不异此。盖月与地能出景者,不在其受光之面,或其左右必于受光反对之面。日光不照之地,在日食则为月景之处,在月食则为地景之处矣。《说》二章。 光景相反图 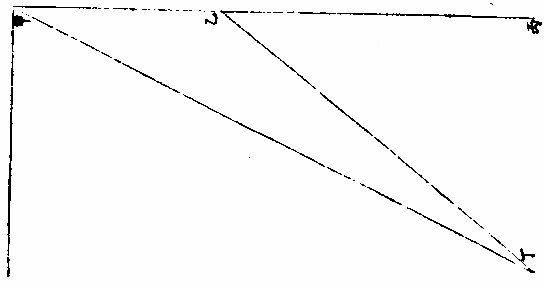 光景相反图说 一曰“景与光所居正相反○”,暗体得光于此面,射影于彼面,是景之中心,与原光之心、暗体之心参相对,如一直线,则暗体隔光于景,使原光之心恒居一线之末界,其正相反之彼界,其景之心在焉。如曰不然,设原光在甲,其照及乙,乙为暗体,隔光生景。据云:“景不射丙。”〈丙者与甲正相对之处〉为甲乙丙直线,而斜射丁则乙甲丁者角也,有角则有几何,凡几何,皆分之无穷,能出直线至于无数,而皆至乙丁边。夫甲既为原光之体,其所照必以直线出之。〈试诸仪器足以为证〉即乙丁皆在受光之地,何自能为乙暗体之景乎?因此明景与光,正在相反之两界。论暗体者,其受光之面,必向光所出之原界,其生景之面,必向景所射之彼界,亦正相反也。论日与月,独至两交之处而有食,亦依此理。 体动景移图 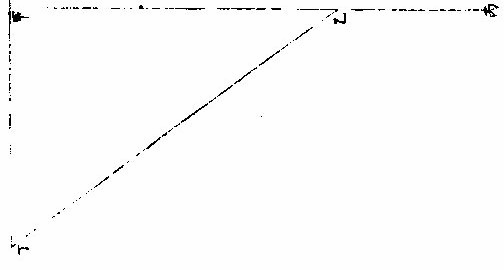 体动景移图说 “二曰,明暗两体,任一运动,景随之移○。试以暗体移动,其所借之光,随处不一,即所生之景,亦随处不一。 盖景与光既如一直线,即暗体所居,定为景之末界。 如直线之首,首移而线尚不移,则是曲线,非直线也。 又试以明体移动,设甲为明体,乙为暗体,乙丙为影,则甲乙丙如一直线。如曰明体,甲移至丁,丁仍照乙,而乙尚射景至丙,则丁乙丙犹直线也,有是理乎?”问:太阳照室,仅通隙光,光照墙壁,奕奕颤动,太阳既自顺行,墙隙仍无迁变,则此颤动为从何来?或者光与景未必定为直线,而能微作曲势乎?曰:“西古博物者亚利斯多言空中尝有浮埃,轻而不坠,微而不显,庄周氏谓之野马,或亦称为白驹。幽室之”内,原光既微,次光反厚,即显此物在于光中,纷入沓出,能乱光景之界,使目视景,絪缊浮动,而寔非景动,乃景之界线,为浮埃所乱,致使其然也。更以气为证,今观太阳出地,地面以上多生蒙气,气在日体与人目之间,即见日之光界,亦如颤动。非独日也,日中晴朗,切视地面,光耀闪烁,如波浪然。炽炭在垆,炭之四周,火光煜煜,亦如颤动。凡若此者,一皆繇气而生。在日在地在炭,固无颤动之理。是以景必系于暗体,如轮必系于枢轴,光上景即下,光东景即西,必相对也,无相就也。 故太阳照地,其光绕地一周,则景在其相冲之界,亦绕天一周。盖日光从其本天直射至于地面,而景在地之彼面,亦直射至于月天,第日体常依黄道中线,则地景亦常依黄道中线,而月行常出入黄道中线之内外,是以月体与地景不得恒相遇合,大都不合时多,合时少,故日月不食时多,食时少,以此。 《景之作用》 月与地,若各以其景相酬报然。如月望,则地景隔日光,令月不受照,有时失满光,有时全失光也。至月朔,则月体隔日光,令地不受照,有处射满影,有处留少光而已。《说三章》。 一曰“月食于地景○。”月食在望,缘日月相对,其理明矣。独谓暗虚为地景者,或致疑焉。今解之,月对日受光,藉非日月之间有不通光之实体为其映蔽,则何繇阻日光之直照?若天体及空中之火,空中之气,皆通明透彻,不能作障,使月失光也。即金水二星亦是实体,有时居日月之间,然其景俱不及地,况能过地及月乎?则知能掩月者,惟有地体。一面受光,一面射景,而月体为借光之物,入此景中,无能不食,半进而半食矣,全进而全食矣。 “二曰日食者,月揜之○恒言。月在内去人近,日在外,去人远,故定朔时,月体能揜日光是已。第金水二星亦皆时在日内,又皆不通光之实体,水星虽小,金星则大于月也,何独月能食日乎?”曰:“二星虽有时在日内,则去人甚远,远则视径见小,不能揜日百分之一二,而日光甚盛,所亏百之一二,非目力所及。且二星比”月去日更近,所出锐角之景更短,不能及地面也。 若月体之大,虽不及太白,而去地甚近,去日甚远,一指足蔽泰山,又何疑乎?由此言之,求一实不通光之体,全揜日体者,惟月为能。又自西而东,不及三十日而周,其行度较于诸天最为疾速。故每望定朔,皆同经度,皆能有食。其不食者,繇距度不及交耳。 三曰“因景之径,生多变易○。月以距度广狭为食分多寡:一因去交有远有近,去黄道中线有正有偏,一因入地景有浅有深故也。”今论其全食者,而大小迟疾,犹多变易,曾非一定。盖日在自行本天,月在小轮,相距远近往往不等。日距月近,“较距远时更照月体之多,分从月体出景更短,其景至地更小,则日虽全食”,月体见小,历时亦速也。日与地亦然,以两体相距之远近为地景之大小。使月食时入于地景,在其近末之锐分,则暗虚之体见小食分少,历时速。皆因三体之相距远近以生大小迟疾。地景、月景皆无一定之径,致令随时变易如此○。若月景、地景二径之小大又自不等。故日食尽于食既而月,则食既以后,尚有既内余分。盖地景大于月景,故两食皆全,其亏复迟疾,无能不异矣。又月食天下皆同,日食则否。日食则此地速,彼地迟,此地见多,彼地见少;此地见偏南,彼地见偏北,无不异也。月食则凡居地面者,目所共见,其食分大小同,亏复迟疾同,经历时刻同,唯所居不同子午线者,则见食之时刻先后不同耳。盖月一入景,失去借光,更无处可见其光也。又概论天下日食,应多于月食,为二径折半,其近交时,加以南北视差,易相逮及。故论一方,则日食应少于月食,为月食共见,日食因地故。 《日月食合论》 日食与月食不同势,食日谓之障食,食月谓之藏食。 何谓“障食?”日为诸光之宗,月与星皆从受光焉。月之食日,非真食日也。《定朔》则地与月与日自下而上为一线相参直。月本暗体,今在日与地之间,以暗体之上半受光于日,以下半射景于地,如屏蔽然,特能下揜人目,而不能上侵日体,日之原光自若也。是故人见为食,而实非食也。何谓“藏食?”定望则日月相对,日光正照之,月体正受之,人目正视之。若于此际经度相及,适及两交,日与地与月亦为一线相参直,而地在日与月之间,地既暗体,以其半体受光于日,以其半体射景于月。若月体全入于景中,则纯为晦魄,必待出于景际,然后苏而生明,如没而复出者然。是则可谓真食也。总之日月两曜,若同行一道之上,则每朔每望无不食矣。日月、地三体,若并不居一直线,则永无食矣。惟各行于一道,时及于两交,故日与月皆隔五月而一食,或六月而一食。岁岁大率有之。不食者半食于夜,日食则此方所见,他方所不见耳。其食也,日体恒居一直线之此界,其彼界则月体地体迭居焉。月居末界,即月面之日光食于地景矣。“地居末界”,即地面之日光食于月景矣。 日月交食总图  日月交食总图说 如上图,“甲”为地,巳为日,卯辰圈为黄道,乙丙为白道,其大距:〈两距之最远〉《五》度弱。〈二分〉丁戊为两交。〈即龙头龙尾亦名罗睺计都〉论《月食》:“日照地球,其光自庚辛至地切两旁过之,而复合于壬。自甲至壬角体之形为地景。地景之心,恒随太阳而行。黄道中线若躔处去两交远,二径折半小于两道之距度分,月行本道,从旁相过,不能逮及,则不食矣。若正遇于两交,或交之左右,二径折半大于二道之距度分,则两相涉入,月为之食。其食分多”寡在距度广狭,距度广狭在去交远近也。论日食则人目所见,恒在地面,推得实会,仍须推其视会,若仅据实会,则是地心之见食,非地面之见食。凡有无多寡,加时先后,悉皆乖失矣。如《图丁》为月,或正居于两交,或在交之左右,日月二径之各半,合之小于距度分,则月能掩日,日为之食,不然则不食也。所谓“实会、视会兼推则合”者,地面所见,推食于地平以上,至天顶之正中,则独推实会,便为视会。自此以外,地面所见,先后大小迟疾渐次不同。如图人在地面,癸依丁月之径,适满太阳之庚辛径,则见为全食。若人在地面,子依丁月之径,乃见两切线所至为己寅,则月掩太阳,止于己庚,半径见为半食矣。大凡日欲食时,月不能离躔道一度强。自此以上,无缘相涉,故定朔之日,有食时少,无食时多也。 太阳本行图  太阳本行图说 甲为地球在天心,其大小之比例,难可计算。略言之,则地之与天,若尺土之与大地也。如图外大圈为黄道,与地同心;内圈为太阳本天,其心在乙,乙之离地心依第谷算,为全数十万分之三千五百八十四,约之为百分之三有半也。其最高今时在鹑首宫六度为丙,太阳右行,从辛过丙,一周天而复于辛,为三百六十五日二十三刻三分四十八秒,是谓“岁实。”《任》躔某宫某度分,皆以地心甲为主,而地心所出直线,至戊黄道,指为太阳之实行。其平行则又以本圈之乙心为主。故人在地所测之实行,时速时迟。而太阳因最高在北任分,本圈则北为大半。故北六宫之日数,多于南六宫几八日有奇也。 依此见求太阳之躔度必用两法:一者定其本行,如随乙丁己直线窥之,从乙心见黄道上之己点;二者定其实行,如随甲丁戊窥之,乃从地心见黄道上之戊点。先得其平行,又以加减求实行,而平实之差为戊巳弧,以甲丁乙三角形求之,即得也。其自丙过秋分至庚两行之差,必减平行而得实行。自庚过辛春分至丙,则加于平行而得实行。若用表,则从丙最高起算,或从庚最庳起算。至日体之本度为引数,以求加减之度。 太阴朔望本行图 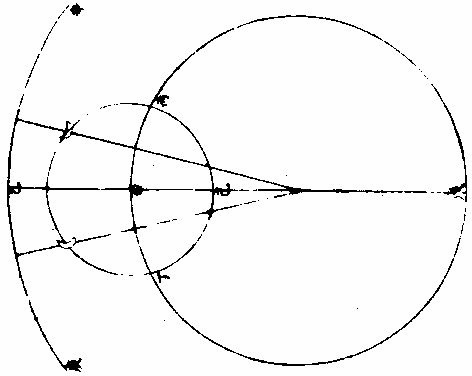 《太阴朔望本行图说》: 月离之术,依《歌》《白泥论》,有本圜,有本轮,有次轮。本轮之心依本圈之边满一转,即次轮之心依本轮之边得两转,故朔望时月体皆在次轮之最近。最近者,近于本轮之心也。因是不用次轮,但以最近处为界,得圆圈。《月离历指》谓为本轮之内圈,此可名朔望之小轮也。 假如丙丁戊为太阴朔望时之本圈,则与地同心。〈因无差故设为同心〉本轮为乙、丙、丁,其心在本圜之边。甲右距日得每日十二度一十一分,其最高在乙,最庳在己。月体又居次轮之边,左行自乙至丙而己而丁,谓之“引数。”最外有黄道为辛、庚。若从地心出直线上至黄道,而次轮心正居此线之上,则所指者为太阴之平行度分也。又从地心出直线上至黄道,而月体正居此线之上,则所指者为太阴实行度分也。凡月转或在高、或在庳,正当一宫初度;〈乙也〉或“七宫初度。”〈己也〉则平行即是实行,过此必有两行之差。则以差数加减于平行度分,得其实行度分。又月在乙丙己半转,则以减得之,若在己丁乙半转,则以加得之,以在朔望。故平实行相距之极大差不过四度五十八分二十七秒。 〈甲丙甲丁是也〉过此为两弦之差,则更少与交食,无与月离。 历详之,若用不同心圈论,则并不用此本轮。其加减平行度分而得实行度分,理则一也○。因日月以平实分本行,故平朔、平望时,两体未必正相合、正相对,凡实会之,或先或后,日月各以其平行直线相遇,而合为一直线,则是中会。 实会中会视会 《测天约说》言“日月之行有隅照。”〈相距三之一〉有方照:〈相距四之一〉有六合照。〈相距六之一〉然悉无交食,而独相会。〈朔也亦名合会〉相对。〈望也亦名照会〉则能有食。故本篇所论者,止于“相会”“相对”也。抑会者,总名也。细言之,有实会,有中会,有视会,三者皆为推步之原。故言交食之术,必先言相会相对,言相会相对之理,必从“实会”“中会”始。 实会中会以地心为主 实会者,以地心所出直线上至黄道者为主,而日月五星两居此线之上,则实会也。即南北相距,非同一点,而总在此线正对之过黄极圈,亦为实会。盖过黄极圈者,过黄道之两极而交会于黄道,分黄道为四直角者也。则从旁视之,虽地心各出一线,南北异纬,从黄极视之,即见地心所出二线,东西同经,是南北正对如一线也,是故谓之“实会。”若月与五星各居其本轮之周,地心所出线上至黄道,而两本轮之心俱当此线之上,则为月与五星之中会。日无本轮,本行圈与地为不同心,两心所出则有两线,此两线者若为并行线,而月本轮之心正居地心在线,则是日与月之中会也。盖《实会》既以地心线射太阴之体为主,则此地心线过小轮之心,谓之“中会”矣。 若以不同心圈之并行线论之,因日月各有本圈,即本圈心皆与地心。〈即黄道心〉有相距之度分,即日月循各本圈之周,右行所过黄道经度,必时时有差。〈与地不同心故也〉“其从地心出直线,过日月之体上至黄道,此所指者为日月之实行度分也。设从地心更出一平行直线,与本圈心所出直线偕平行而上至黄道,此所指者为日月之平行度分也。”盖太阳心线与地心一线平行,太阴心线亦与地心一线平行,恒时多不相遇。至相遇时,两地心线合为一线,则是日月之中相会。若太阳实行之直线与太阴实行之直线合为一线,则是日月之实相会。合会、“望会”,皆有中有实,其理不异。 实会中会图二 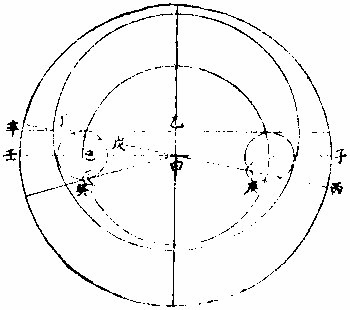  实会中会图说 先依小轮法作图甲,为地心,亦为黄道心,亦为太阴本圈心。〈太阴与地同心者为用本轮故盖本轮周即太阴圈心绕地心之周其理一也〉乙为太阳本圈心。〈与地不同心〉“太阳在丁,太阴在戊”,甲戊丁线直至黄道圈得辛,指日月实相会之度。如太阳在丁,太阴亦在甲辛直线上为庚,而此线至黄道圈得丙,即指日月实相望之度。若太阴在癸,与太阳不同一线之上,乃过月本轮之心己而至黄道壬,此直线所指,则日月中相会之度也。如月在庚,从地心出并行线,甲子与甲壬太阳平行为一线,而至黄道,子亦指日月中相望之度矣。 次依不同心圈法,如后图黄道与太阳之本圈皆同前,独太阴无本轮而易为本圈,其心与地心不同,在甲乃在丙,此亦以日月并居一直线为实会。如太阳在丁,太阴在本圈之边戊,地心所出甲戊,丁线至辛,则所指为实会。而正对月体,至黄道寅,则所指为实望。若中会中望则以并行线为主。盖甲壬为地心所“出直线,既偕太阳本圈心所出过日体之直线,乙丁为并行线,又偕太阴本圈心所出过月体之直线,丙庚为并行线”,则是两偕行之直线合为一,甲壬而至黄道,故所指者为日月中相会之度也。其至相对之黄道上为癸,则所指者为日月中相望之度。设过此交会之时,太阴在丑,则月圈心出者为丙丑线,地心出者为甲己线;两线自偕为平行,而甲壬与乙丁自偕为平行,甲壬甲己不得合为一线矣。故地心所出之两偕行线,能合为一甲壬者,必指中交之度,为日月相会之共界也。 《见食随地异时》 月食分数,天下皆同,第见食时刻随地各异,何也?人各就所居之地,目力所及者,则见月食,而各所居地皆以子午正线为主,若其地同居一子午线者。〈南北地纬虽异东西地经则同〉“则所见月食之分数迟速皆同也。若地易子午线易,则时刻并易矣。所以然者,时刻早晚,因太阳行度随人所居,各以见日出入为东西、为卯酉,即以日中为南为子午,而平分时刻。故月食时必本地之日未东升或已西沉,乃得见之。若在其昼,时刻不可得见也。天启三年九月十五夜望,月食顺天府及南北同经之地,则初亏在酉初一刻一十二分,食甚在戌初初刻,复圆在戌正二刻一十三分,各筭外。”高丽及其同经之地,即初亏在酉末戌初。而西洋意大里亚诸国,日尚在天顶为午正,则不见月食。以里差推之,西洋之初亏在巳正三刻四分,食甚在午正一刻七分,复圆在未初三刻一十分,各算外。虽月入景七分五十六秒,所居宫度彼此远近皆同,而以里差,故彼地彼时太阳在午正二十二分,太阴反在子正二十二分,食甚正在日中,何从见之?今壬申年九月十五日夜望月食,初亏在卯初三刻,则陕西、四川等处得见,南京、山东等近海东境不可得见也。秦、蜀之子午,异于东方之子午,故 今以顺天府推算本食,因定各省直之食时,宜先定各省直视顺天子午线之里差几何,后以其所差度数化为所差时刻。每一度应得时四分,向东以加,于顺天推定时刻,向西则减,乃可得各省直见食时刻也。若日食,则其食分多寡、加时早晚,皆系视差,东西南北,悉无同者。必须随地考北极高下,差其距度,随地测子午正线,差其经度,乃可定其目见器测之视时。定子午术,见《西测食略》。中法于当身所居目见器测考定一月食之时刻,与先所定他方之月食时刻较算。或两地两人同测一月食,彼此较算,乃以所差时刻得所差度分也。 “前顺天府所推月食时刻,并具各省直先后差数,因未得诸方见食确数,无从遽定地之经度,但依《广舆图》计里画方之法,略率开载耳。”既而咨报多相合者,然非甄明之辈躬至其地,测极高下,见食早晚,终未敢以耳闻臆断,勒为成书也。左方所记,政所谓略率开载者,欲求决定,当竢异日,故称约加约减焉。 南京应天府及福建福州府约加四分〈凡一十五分为一刻〉山东济南府约加五分。 山西太原府,约减一刻〇九分。 湖广武昌府、河南开封府约减一刻。 陕西西安府、广西桂林府,约减二刻〇四分。 浙江《杭州府》约加十二分。 江西南昌府约减一十分。 广东《广州府》,约减一刻〇五分。 四川成都府,约减三刻〇七分。 贵州贵阳府约减二刻〇八分。 云南,云南府约减四刻〇八分。 |
| 梦远书城(guxuo.com) |
| 上一页 回目录 回首页 下一页 |