图书集成·月部汇考二(4)

月部汇考二(4)

　　《论月光》

　　太阳为万光之原本，其体至实。

　　光大小，因体虚实。如炼铁之光，大于炼炭之光，铁体实于炭也。

　　其质极纯，〈质不纯者光亦不纯则不能大〉其体为“《全球》曲面。”

　　凡发光者，不论曲面直面，必须顺平。若凹凸之面，不能发大光，稍有偏欹，光则相夺，亦不能大。

　　故在《大圜》中为“大光”之独体，月及经纬诸星之光，皆从禀受焉。〈月借日光古语则然〉何以明之？如月食甚时，地球隔太阳之光，露光极微，目所难见，一也；日食甚时，月在日与人目之间，月之下魄不受日光，人目见之则为黑色，二也。

　　问：“月既无光，乃两食甚时亦有淡光，此为何故？”曰：“体实无光，而能受光，而能发光。两食之时，不受日光，而经纬诸星亦能映照，相受相发，因生微光矣。”

　　月光有二：一为对日而发光，名曰“正光”；一为日光不至，而从所受之处相映发为微光，名曰“次光。”

　　月受日光大半图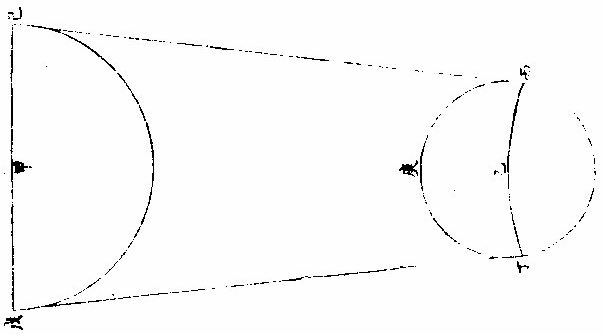

　　

　　《月受日光大半图说》。

　　问：“月近日人见光小，远日人见光大。何故？”曰：“月合朔时，外大半受光。”

　　“日体大，月体小”，则日必照月之大半。

　　人自下土止，视其内小半则无光，既而生明，所见渐大，至一象限则已见其受光之大半，故渐远渐大也。

　　何谓日照月之大半？如图甲为日，乙为月，戊丁己丙两光线切月体，从丙从丁向乙，作两垂线，成戊丁乙己丙乙两直角，则丁乙乙丙两线不成一直线。何者？凡一直线截平行两线，其内两角并与两直角等，反之，若两直线不平行，即一端渐近，一端渐远，其渐近内两角，必大于两直角。今设丁丙两直角，则丁乙乙丙不能以一直线与乙为角，若从乙心作径线，必在丁丙两点之上，则丁庚丙必月周之大半矣。

　　月近日受光之分大，远日受光之分小。

　　月体自无运动，曷知之人所恒见，斑驳之象，终古不易。

　　月近日受光分大远日受光分小图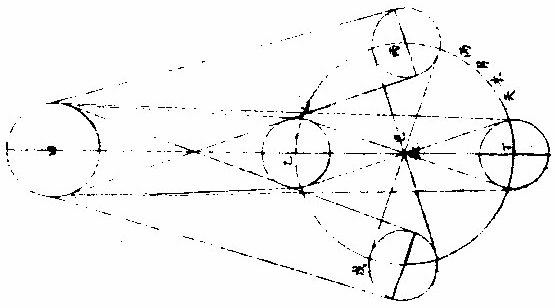

　　

　　《月近日受光分大远日受光分小图说》。

　　“月朔时，上大半为明，下小半为魄，月望时，上小半为魄，下大半为明”，两弦各明魄半也。如图甲为日，乙丙丁戊为月，本天人在地为己。月或上或下，恒半为明，半为魄，从人目作视线，自见月距日近光小，距日远光大。

　　从“生明”以后渐长，生魄以后渐消，

　　人止见月体之小半，人目一点也。从点作两线，切一圈，两切线之内，弧必圈之小半。〈如图〉

　　如上言，日照月得大半，人见月得小半，则定望前后各数刻，月犹能发全光，满大半之限，然后魄生而光减，非若晦朔之间，一瞬即生明也。

　　月去地有高卑人目所视有远近图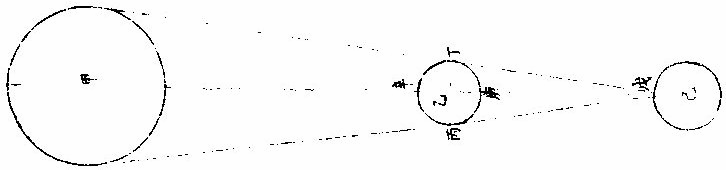

　　

　　月去地有高卑，人目所视有远近《图说》。

　　问：“日照月人见月各几何数？”曰：“日月去地去人，各有高卑近远不等。古法分月体周为三百六十度，折中推得日照月为一百八十一度六分度之一，人目见月为一百七十八度四分度之一，日照地为一百八十〇度二十五分半。”

　　“月体地球”，其周分为三百六十度，与天等；

　　如图甲为日，乙为月，己为地，日月之视径约等。〈月在最高日在最高冲〉人目在戊，则戊丙戊丁两视线，定见月之丙庚丁弧，从月心乙向丙向丁，作乙丙乙丁两垂线，成乙丁戊丙斜方形，从乙戊平分之，作乙丁戊直角形。

　　形有丁戊乙角一十五分四十〇秒。

　　日月视径，并约为三十一分二十秒。

　　即丁乙戊角，必八十九度四十四分二十〇秒，其丁庚为见月之半，弧倍之，得一百七十九度二十八分四十〇秒。

　　若月径为二十八分，则所见弧之小余三十二分；若月径为三十三分，则小余二十七分。

　　因上图推合朔时日照丙辛丁弧，丙辛丁者，丙庚丁之余也，是为一百八十〇度三十一分二十〇秒。

　　用日距地之数及其比例，推得日照地为一百八十〇度二十五分三十六秒。

　　月上下弦前后人所视有曲直线图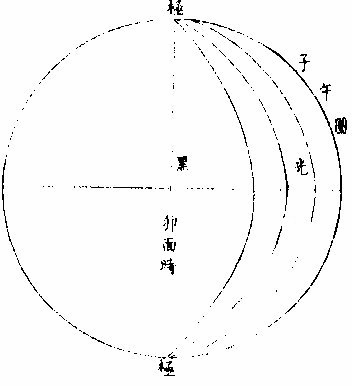

　　

　　月上下弦前后，人所视，有《曲直线图说》。

　　问“月生明后，其光曲抱月体，至上弦下弦明魄之界则为直线，望前望后，明魄之界，又为弧曲之线，何故？”曰：“月本球体，人目所见，似为平面，其理正如平仪。然仪之子午圈，可当月周，皆大圈也。仪之极分交圈，可当上下弦，明魄之界，皆直线也。仪之时圈可当太阴。

　　每日距太阳渐长渐消，明魄之界，皆弧曲线也。凡仪”上大圈，皆分球为两平分，其全见者独子午圈耳。他诸圈皆半见半在仪之彼面，彼面者在月，则为上半球也。〈人所不见〉平仪曲线：〈实时线〉本是大圈斜络于球，止见其半，故为不等。撱圈之半。

　　人视之为“撱圈”，渐消渐长，故不等。

　　月面《中明魄界》之弧曲线，本亦大圈，因其斜络止见为半，亦不等撱圈之半也。

　　其与平仪本理未能全合者，仪上圈皆分球为两平分。此依上言，月受光者大半，不受者小半，则明魄之照界别成一小圈，为大圈之距等，而非月球之中圈。

　　中圈必大圈也。分球为两平分。人目所见之界，其直线则距等圈之似直线。〈本是圈也人视

　　为直〉其弧曲线，则亦距等撱圈之半也。以此之故，朔后三四日，新月之两端，能过半周之界。

　　月光日所照与人所见时各不同图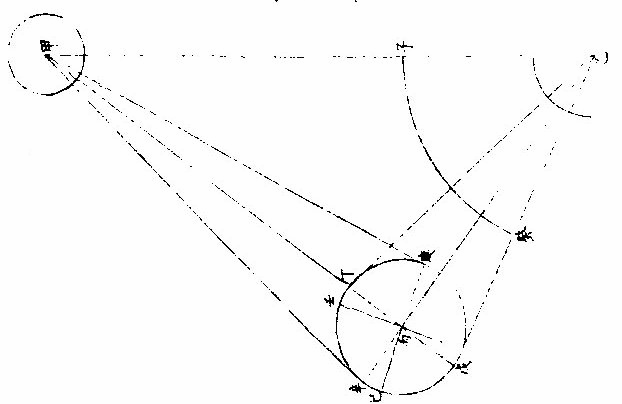

　　

　　月光日所照与人所见时《各不同图说》。

　　问：“月行每日去离太阳约十二度等也。然朔前后光魄消长之分数少，两弦前后消长之分数多，望前后复少。人于定望前后一二日见月光如不易，何故？”曰：“月礼本圆，圆面之上必有两圈，皆为明魄之界，一为日所照之界，一为人所见之界，两圈于定朔时相合为一。”〈照与见相反〉定望时亦合为一。〈照与见相同〉过朔望，渐相离。

　　如两交圈结于两极，渐展渐离相离之处，若黄赤二道之距远度也。

　　两界圈之距间，则人所见月体有光之分也。以此推之，人目所见为球之正面，如平仪之极分交圈也。两界合圈，在球之侧面，如平仪之子午圈也。初日相离距度若干，人侧视之则见少；如时圈之近子午度分等，人侧视之则见狭。两弦时距度亦若干，人平视之则见多，如时圈之近极分圈度分等，人平视之则见广也。故朔望之消长非少而见少，两弦之消长非多而见多也。如图甲为日，乙为地，丙为月，丁丙戊庚为人所见月之半，己丙庚丁为日所照月之半，丁庚为两界之距间，即本时人见月体有光之面也。

　　从目日及月心，作甲乙丙三角平面平分月体则己丁庚戊为圆面。

　　甲乙丙角形有甲乙。〈日距地心〉约一千二百地半，径，有乙、丙。〈月距地心〉约六十地半径，又有甲乙丙角，为月距日之度。〈试作癸子弧即得乙角之度〉求丙甲乙角设月距日之乙角，为四十度算，得一度五十五分，以并四十度，得四十一度五十五分。又引长乙丙戊，甲丙辛外角，即与丁丙庚角等。

　　庚丁壬丁壬辛，皆四分之一，各减共享之，丁壬，其两余等。

　　甲、丙辛外角与相对之两内角等，即丁庚弧亦与两内角等，则月距日四十度。人所见月体有光之分，约得四十二度。

　　言“约”者，未定之辞也。如上论月体明魄两界圈似大圈，而实距等圈则有差。又约月距地为六十地半径，然时多时少，日距地为一千二百地半径，亦时多时少。又月经度距日四十度，或在南或在北，亦有差，是故约言之。

　　若测得月体明魄两界之比例，可推月距日之度，即上《图说》反用之。

　　每日月面光界图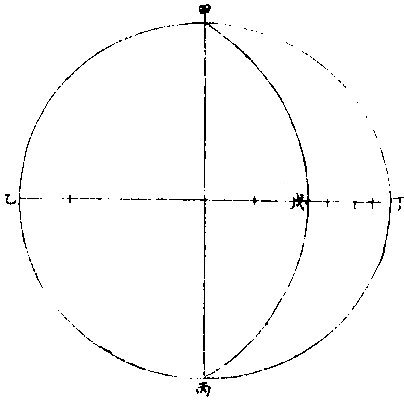

　　

　　每日月面《光界图说》。

　　欲图某日之月光界，先求月距太阳若干度分，次依上法求月面半径上明魄界若干度分，从两极。

　　月面上两极定为过白道，两极之大圈线，或与白道为直角。

　　作撱圈之半，乃本日所见月面有光之界也。若未至九十度，光作角形，若过九十度，作未成圆形。如图甲丙为月之两极，丁戊为明魄之界，甲戊丙线为本日之月光界，甲戊丙丁为两角之形，甲戊丙乙为未成圆形。

　　用上法推凡日光界为全径。

　　十分之一，距日二十六度；
　　十分之二，距日四十度半。
　　十分之三，距日六十度；
　　十分之四，距日七十二度半。
　　十分之五，距日九十度弦也；

　　十分之六，距日一百〇七度半。
　　十分之七，距日一百二十度；
　　十分之八，距日一百三十五度半。
　　十分之九，距日一百五十四度。
　　满十分距日一百八十度，望也。

　　以上数依《目测》为定。若推算当求月高卑，求白道纬度，当有微差。

　　月望光色中边有浅深图

　　月朢光色中边有浅深图

　　《月望光色中边有浅深图》说。

　　问：“月望时，中心光色稍浅，四周光色特深，何故？”曰：“月体圆，中心体一分发光一分，四周体三分发光一分。

　　一分者，所受日光少，故发光浅；三分者，所受日光多，故发光深。”如图甲为月体，乙为目，见月之角，从角分为十分，中一分见月周一十一度有奇，旁一分见月周二十五度有奇。

梦远书城(guxuo.com)