古今圖書集成·乾象典第三十七卷

第三十七卷

　　月部彙考二

　　《羅雅谷月離曆指》

　　《月離各種行度》

　　月離行度與日躔異，日躔恆依黃道，其行度三而已。

　　隨宗動天西行，一也；「自行」，二也；最高行，三也。若月離則有七種行度。如左：

　　一曰「隨行」，隨行者自東而西，依宗動天，一日一周，七政恆星共繇之。其起算之界，為子正初點或午正初點，與太陽同。

　　二曰「平行。」〈一名本行〉平行者，月之本天自西而東，日平行一十三度有奇，二十七日有奇，而行天一周。其界有二：一以太陽為界，從合朔起算，每日去離太陽若干度分，以命太陰之本行度分。累積之，一以宮次節氣為界。

　　宮次如降婁、《大梁》等，節氣如春分、秋分等。

　　從各初點起算，每日去離若干，以命太陰之本行度分累積之，此行謂之「交周」，滿一周為交終。其初交曰「正交」，其次交曰「中交。」其行各及半，曰正半交，曰中半交○。其兩界命兩種行度分異名同理。

　　三曰「自行。」

　　一名「本輪」，舊名「小輪」也，因小輪非一，故改命之。

　　「自行」者，太陰之行，不平不順，有時疾，有時遲，既而紛紜，無憑布度《古曆》因想近月四周有一本輪太陰，既隨本天循交道。〈即白道〉東行。〈右旋〉又「依此輪自東而西。」〈左旋〉一日行十三度有奇，二十七日有奇，而行輪一周，此亦平行也。而與交道平行參錯不一，所以下土視之，時疾時遲矣。因其疾遲以別於交道之行，故彼名平行，此名自行也。既曰自行本輪，則疾時與交行相合，遲時與次行相背，亦宜如五緯之法，有逆行度分。此獨言遲不言逆者，月行甚疾，但見其遲，不見其逆也。

　　此周謂之轉周，滿一周為轉終。分四象限：首限曰正轉，二限曰正半轉，亦曰本輪之最高。三限曰中轉，四限曰中半轉，亦曰本輪之最庳、曰最高衝。〈或省曰高衝〉行最高極遲，行最庳極疾也。

　　最高最庳之一周，又名「不同心圈」，其與本輪異名同理。

　　四曰次輪。次輪者，太陰之最高，既依白道行，則月離最高時，其距地心之遠近宜等。迨測之，則時時不等。

　　古曆又想本輪之周，復有一次輪，循本輪左旋，月在次輪之上，循周右旋也。此法古曆所未有，以意命之。

　　其行次輪一周，名為次轉終也。四分之，則為小四象：第一名正初象，第二名正半象，第三名中初象，第四名中《半象》也。

　　五曰「交行。」交行者，從測候見太陰行白道。

　　古法月有九行，殊謬。《元授時曆》廢不用，獨言「白道交周」是也，一名月道。

　　出入黃道約五度有奇，不行黃道中線。

　　何名黃道中線？七政恆星，皆循黃道行，而六曜皆有出入，如太白最遠，出入約六度，故黃道左右廣十二度，名為「黃道帶」，而太陽獨行其最中，故名中線也。黃道一名躔道。

　　而兩交於中線。兩交之點，一名「正交」；〈亦曰羅㬋〉一名《中交》。

　　〈亦曰計都〉兩交之行，自東而西，與他行異，亦名《羅計行度》也。

　　六曰「又次輪」，古來無有也。萬曆間，《西史》第谷測候極密，得太陰行兩小輪。〈其一本輪其一次輪〉其各兩半時。〈兩小輪各有正半中半〉之兩均數，與實測之度分，往往未合，故知次輪而外，當有又次一輪。此之為數，微眇難分，其於曆法未關損益，故無暇及也。

　　七曰「面輪。」面輪者，太陰既依本輪，又依次輪，各周行即月，面宜恆向次輪心。下土所見，時時旋轉，須當不一，若之何終古恆如是，故當復有本行，使面恆下向也。此亦未關疏密，不復備著。

　　日月視徑大小圖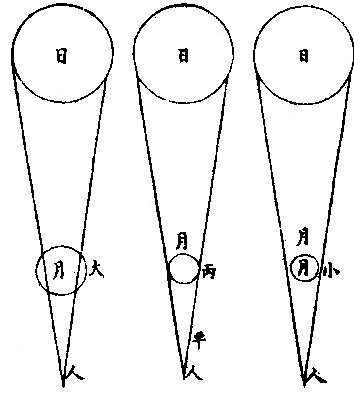

　　

　　《日月視徑大小圖說》。

　　《古史記》「日食既者，或言晝晦，恆星皆見，鳥棲獸宿，或月不盡掩，日有金環。」

　　如中圖，月全掩日，即其似徑與日似徑等，此則食既於東，生光於西，既與甚同時，不移晷也。如右圖，月體不足，掩日則有金環，月之似徑為小。如三圖，則食既以後，更有食甚，久而生光，月之似徑為大。所以然者，日在最高，月在本輪最卑，日高故視徑小，月卑故視徑大，則掩日有餘也。日在最卑，月在最高，日之視徑大月小，則掩日不足也。俱在最高，俱在最卑，故兩視徑等，則掩日適足也。

　　《日月之視徑與實徑大小絕異》

　　是，其徵有七。凡視徑。〈與似徑同〉「時見大，時見小」，必非其實也，視也，一徵也。即有時等，而日在上，去人遠，月在下，去人近，則日之實徑必大，月必小，二徵也。月掩日下土所見九服各異如此。方此時日全食，南北相去四五度。〈二百五十里為一度〉「即不見全食，東西同時亦不見全食。」是則月入地球為小，地視日亦小，月視日更小，三徵也。地景短，不能食熒惑，何况歲星已上，則地小於日，月過地景則食，食時見月，小於地景，則更小於日，四徵也。七政各有性情，能力施暨下土，其勢略等。乃其視行有疾有遲。行遲者，其天周大；人見為遲，本行自疾。所以然者，遠故也。近者行疾，其天周小，如舟行大水，遠見行遲，近見行疾，因是能力所施。近而疾者，其見功亟；遠而遲者，其見功緩：五徵也。月距日九十度，其光過半圈，則「發光之體大，受光之體小」，六徵也。因上推月距地為地全徑者三十，日距地為地全徑者六百○五，則日比月，天其大。〈算周〉約二十倍日本天半度，月本天半度，則其比例「為一」與二十七徵也。

　　《月天視七政天為小去人最近》

　　曷知之？以交食知之。凡言食者，物在於彼，有他物隔焉。或虧或蔽，則謂之食。所食者必遠，能食者必近也。

　　所食者必在外，能食者必在內也。以球論，則內近心者必小，外遠心者必大也。試觀月掩日，日為之食，日外月內，不待言矣。月掩恆星，星為之食，星外月內，不待言矣。獨月與五星，曆家言有時星食月，有時月食星亦未然也。夫星固未始有在月下者也。歷稽古史，多言月食五星，而不言五星食月，斯著明已。

　　求月之實徑圖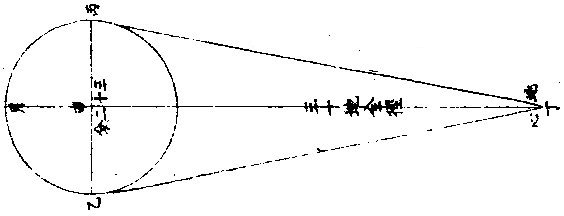

　　

　　求月之實徑圖說

　　測月之實徑用地徑，古法也。今依《歌》「《白泥術》，月平。」〈雨雷際〉距地度為三十地全徑，又四之一，其視徑三十二分二十八秒，推算如左：

　　如圖丁為地心乙，甲丙為月徑三十二分，丁甲為月距地三十，地全徑成甲、丁、丙三角形，有角有邊。求乙丙，得千分地全徑之二百七十六弱，為月全徑。約之得月，一地三倍有半強。若以周徑法求之，則七。〈徑也〉與「二十一」，〈周也〉若六十○半地徑。〈月天之半徑〉與月天之周，依法算，得一百九十。地徑又七之一，以三百六十〈天周平度〉而一，得一度，為三十六分地徑之一十九。次以六十分為一率。〈六十分一度也〉三十六之一十九為二率，三十二分為三率，求得二千一百六十分地徑之六百三十六，約得二十四之七或三有半之一，同上率。

　　若用月五限數，所得大數同上，零數小異，不足算。

　　《定月實徑里數》

　　天度里差，古今不一。今約定南北二百五十里而差一度。以天周三百六十乘之，得九萬里，求徑，得二萬八千六百四十八里，以日十數。〈地一日五又百之四十三〉乘地徑之里數，得日之實徑為一十五萬五千五百六十五里。月之實，徑為地徑千分之二百七十六。以乘地徑之里數，得七千九百○七里。

　　《總論月天象數》

　　分別太陰象數，凡為球體者四：第一與第二為表裏，皆與地同心；第一球之大圈；〈一名中圈一名腰圈〉為「白道。」白道與黃道兩交，而分為斜角。兩交之處，一曰正交，一曰中交。第二球者，復球也。復球以外，大球以內，函兩小輪焉。小輪之大者，為第三球，名曰「本輪，亦曰自行輪。

　　輪之徑，為兩大球之距。小輪之小者，為第四球，名曰次輪。」

　　月行九道圖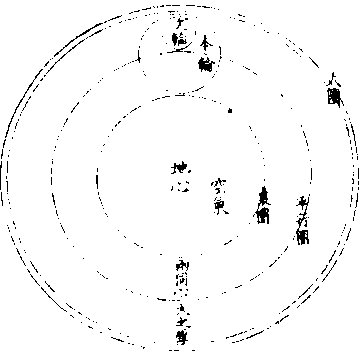

　　

　　月行九道圖說

　　如圖外大圈白道也，又名「月天大圈。」〈包他輪其中〉又名《斜圈》。〈斜交于黃道〉亦名《交周》，亦名龍頭、龍尾之圈。

　　正交為龍頭，中交為龍尾。本圈兩交黃道，其兩交點時時遷運。

　　亦名《九道》。

　　一，白道也，在黃道之四方，皆有內外，并黃道為九焉。元以來，不用此術。

　　「表裏二天」，中容小輪，一體左旋；〈如宗動天行與七政違行〉小輪從之，一日行三分一十秒四十七微，一平年。〈三百六十五日〉行一十九度一十九分四十三秒，凡六千八百九十三日有奇而一周。

　　黃白道極圈圖

　　

　　黃白道極圈圖說

　　四球合體，總名曰《月本天》。其南北二極，距黃道二極各五度有奇。

　　上論「黃白道相距或內或外，最遠者五度有奇。」

　　夫黃道行天，不以黃道極為樞，而以赤道極為樞，故黃道極去赤道極二十三度有奇而環行，名曰「黃道極圈。」月道行天，不以白道極為樞，而以黃道極為樞，故白道極去黃道極五度有奇而環行，名曰「白道極圈。」

　　如上圖，圖有兩黃道，其外則外天黃道或「日天」，或「宗動」，任意取之。

　　月本天中自有三行：一曰交行，二曰本輪自行，三曰次輪自行。三行各有軌轍。其轍跡安在？在其大圜平面也。何謂大圜平面？如本天白道為大圜。〈球之腰圈最大〉從《白道》判本球為二，即所判之處為兩大平面，交行在其周，本輪、次輪行皆在其面也。

　　兩交，一名正交，一名「中交。」月在正交，向黃道內行九十度，謂之正半交，此半周謂之「陰曆，過半周，為中交向黃道外行九十度，謂之中半交，此半周謂之陽曆，過半周而復於正交，為交終西曆，謂之「龍頭龍尾。」蓋兩道間成蟠曲之形，腹粗末細，有若蟲蛇，非謂有龍食月，如俚俗之說也。又謂之「登降之交。」月行黃道內，自南之北，漸高於地平，則言「升」；行黃道外，自北之南，漸向地平，則言「降。」或稱「外內」，或稱「上下」，其義一也。若「羅㬋」、「計都」之名，非古曆所有，疑出於《九執》。唐人再用《九執曆》，僧一行寫之而未盡，陳元景爭之而不得，獨兩《交》猶仍其譯言耳。

　　月平行圈圖

　　

　　月平行圈圖說

　　平行圈者，太陰全天表裏二球之中圈也。與地同心，為本輪心平行之軌道，故名「負小輪圈。」其行順七政右旋。〈自星紀至元枵也〉其界有三：

　　第一，以節氣為界，如冬至、春分等。〈或以宮次〉一，日行一十三度一十分三十五秒○一微，為月之距節平行分。

　　〈止右旋一行〉滿一周得二十七日三十○刻一十三分○五秒，為交終。

　　第二以太陽經度為界，太陽平行經度，日五十九分○八秒二十○微。月之日行多，太陽之日行少。以少減多，得一日之相距一十二度一十一分二十三秒四十九微。滿一周又逐及於日，為朔策。

　　或會《朢策○》，太陰距太陽行二十七日有奇，而一周其間太陽亦行二十七度有奇，則太陰行一周外又二十七度有奇，而逐及於日與之會，共為二十九日有奇也。

　　第三以正交為界，正交逆行；〈左旋〉太陰順行。〈右旋〉一向左，一向右，兩相違背，故距交一行，謂之「雜行。」兩行相并，

　　正交行三分一十一秒，太陰行一十三度十分三十五秒。

　　得一十三度一十三分，四十六秒。

　　月自行輪周圖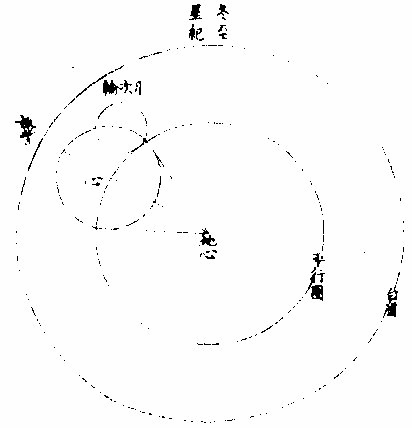

　　

　　月自行輪周圖說

　　自行輪周為次輪心平行之軌道。〈即本輪〉次輪行於本輪周，左旋。〈與七政違行以本輪之最高為界〉初《逆行》。〈向左約九十度留際轉初〉轉順行。〈向右至半周過最庳留際轉中〉復逆行如圖。月在次輪周。從地心作兩線切。本輪周也。〈月在本輪上半周兩切線外日逆下半周兩切線內曰順〉若月在心線。〈從地心過本輪心是為本輪之最庳〉兩行。〈平行自行〉度分等，若在心線前，或後兩度。〈視經度平行度〉必不等次輪，心從最高算日行。〈一十三度三分五十三秒五十六微〉為轉度分，而一周為轉終度分也。〈二十七日五十二刻一十一分五十四秒為次輪心從最高行一周而復于故處〉

　　月次輪圖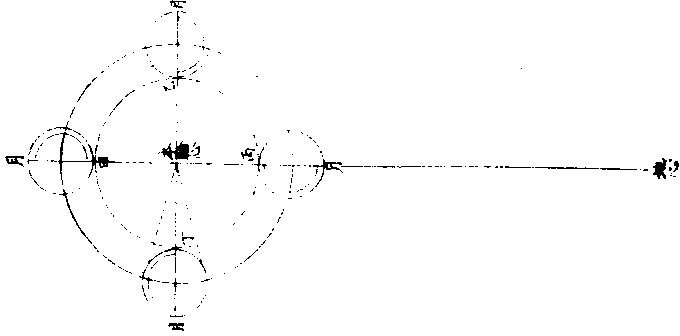

　　

　　月次輪圖說

　　次輪者，月體所行之軌道，其界向本輪心為最近，界之衝為最遠。試以一線聯兩心線，即其界矣。〈如圖甲丙乙丁線〉「月體在次輪近地心半周，即月體逆經度行而順本輪行。若在其遠地心半周，即月體順經度行而逆本輪行。從本輪心出兩線，切次輪兩旁，即定本輪心第二均加減之界○。」如上《測月行諸論》，以定朔朢，則用一自行之均數足矣，為朔朢時，月體必在本輪內甲乙丙丁圈上故也。去離朔朢，宜用兩均數，自朔至朢、朢至朔，必行次輪一周而復。故月實行距太陽一百八十度，行次輪一周三百六十度，而次輪周之日行度，必倍於距太陽之日行度，每日得二十四度二十四分四十七，秒三十微。行一周為一十四日七十三刻七分有奇，半月之率也。〈天上周圈不論大小皆平分三百六十度〉凡月行距日九十度。〈兩弦〉次圈周行半周，在次輪最遠，而距平行經度為極遠。如上圖小輪上之月體所麗，為視行平行之極大差○。因上兩小輪行度，在本輪有最高最卑，在次輪有最近最遠，定為自行之四限。

　　月次輪高卑遠近圖

　　

　　《月次輪高卑遠近圖說》。

　　凡月在次輪上，最遠。〈遠近以去離本輪心論〉次輪心又在本輪之最高，則月距地心為極遠，圖為甲。月在次輪之最遠，次輪心在本輪之最卑，則月距地心為極近，為乙。

　　若在次輪最近，本輪最高，則為次遠，為丙；在次輪最近，本輪最卑，則為次近，為丁。因此四限屢變，視行之勢也。惟朔朢時，月恆在次輪之最近。

　　《論太陰晦朔伏見》

　　太陰晦朔伏見，古今立論，疏密迥殊。漢儒《洪範傳》曰：「晦而月見西方，謂之朏。」〈亦曰朓〉「朏者，政緩所致；朔而月見東方，謂之側匿。側匿者，政急所致。夫晦在朔後，晦失也；朔在晦前，朔失也。曆則失之，而歸咎于政，誣甚矣。」唐曆家以晦日之晨，月見東方，因立進朔之法，使月隱晦晨，明藏朔夕，此則鉤索未能，而妄生遷變。使月有兩朔，食乃在晦，將誰欺乎？《宋、元史》皆非之，頗為辨晰，然未能縷形其所以然也。夫月距晦朔，見有疾遲，因乎天度，因乎地度。即此方近處，合朔于亥子之交，而甲日之晨，乙日之夕，兩見微明，亦時有之。此之進退，將安往焉？况海以南數千里，則有甲晨乙夕，終歲恆見者；漠以北數千里，則有朔在午中，朝暮皆見者。亦將使晨隱夕藏，其可得乎？今法若時若地，應速應遲，皆從籌算可密推；用儀器可指數。先事可豫言，臨時可確按，又何庸轉移避就為也。以此備述所繇，徵之度數如下論：

　　問：「太陰合朔以後，恆以三日見於西方，亦有二日者。

　　其在晦以前亦如之，何故？」曰：「是其因有三○：一、因赤道上之黃道升降度，有正有斜。正升則斜降，斜升則正降。正升斜降者，秋半周六宮。」〈秋分左右各三宮〉是也。「斜升正降」者，春半周六宮。〈春分左右各三宮〉是也。〈皆論斜球非正平球〉「正升」者，赤道之升度多，黃道之升度少。「正降」者，赤道之降數多，黃道之降數少，斜升、斜降則反是。

　　「凡南極出地者」，與上《論》悉相反。

　　若太陰離正降六宮，則朔後疾見。若離斜降六宮，則朔後遲見。其在晦前亦如之。《離》正升六宮則遲隱，離斜升六宮則疾隱也。

　　月行黃道斜升正升圖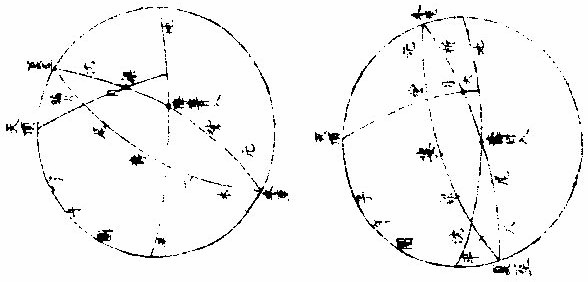

　　

　　《月行黃道斜升正升圖說》

　　如二圖各有子午圈，有地平、有極出地等，有黃道宮。

　　次二圖上圖月離大梁為正降宮，次距太陽十五度，日入月在地平上為十三度半，即能見。下圖月離大火為斜降宮，次距太陽十五度，日入月在地平上為十度，即不能見，一也。

　　月視行遲疾圖

　　

　　月視行遲疾圖說

　　一因白道南北如圖設月距黃道五度，距太陽皆十五度，而緯分南北。

　　日月各有一日所行之軌道，即赤道距等圈也。今如圖設黃道左右五度各一圈，交於距，等月在焉，兩月各至地平，其弧有大小，則入地有先後，人見有遲速。

　　若在北，即入地後黃道疾見；若在南，即入地先黃道遲見。二也○。一因月視行度。若視行為遲段，則朔後見月遲；為疾段，則朔後見月疾。三也○。右第一，因月之見界，以十五度為限。其疾者，朔後一日又四分日之一而見也。若三因并合，又不待此。如合朔在亥子間，則甲日太陽未出，亦見東方；乙日太陽已入，亦見西方。何以徵之？設月在黃道北五度，太陽躔實沈一十五度，本地北極高四十度，即晝長。〈甲之日也〉五十九刻。

　　〈日九十六刻〉加一日刻。〈甲之夜乙之日〉共一百五十五刻。〈甲晨至乙夕〉於時月行約得二十三度平分之。〈合朔前後〉得一十一度半，以加實沈十五度。〈日躔也〉得實沈二十六度半，是乙日日入時月之距日經度也。以減十五度，得實沈三度半，是甲日日未出月之距日經度也。日躔實沈十五度，其斜升五十三度一十三分。月離實沈三度半，又北距五度，其斜升三十六度半。日月兩升度相減，得一十六度四十三分，為甲日之晨日月赤道上出地平之差。〈月先日後〉變時為月出四刻半，而日出得見月東方也。乙日太陽正降為九十五度，月離實沈二十六度半，其正降為一百一十三度，兩降度相減得一十八度，為乙日之夕，日月赤道上入地平之差。〈日先月後〉變時為「日入五刻」，而月入得見月西方也○。若日躔冬至，月離黃道，南推日月出入之差，不過八度，變時為二刻則「不見。」

　　一，系凡極出地愈高愈疾，見因斜升度之差為多，否則遲見。

　　《二系》極甚高，朔後數日不見。

　　《三系》月，距黃道南五度，若極出地六十二度，月盡夜不見。

　　四系極甚高，合朔在午正，則一日之間，晨見東方，夕見西方。如極高五十二度躔離度同上，推得日月升降差一十二度，時為三刻，皆在月見界之內。

　　《五系》既定，月之見界，為距日十二升度，亦可推遲見之日數。如極出地四十度，日躔降婁，月南距五度，推得兩斜升差為一十二度，即得月距日之經度，為四十度。月行當三日有奇，則朔後三日有奇而見月西方，晦前亦如之。

　　三因之外，又有兩因：一曰「朦朦分。」〈即晨昏度一名昧爽黃昏〉日入地平下一十八度為朧，朧之未分，因升降有正斜，斜又有大小，則月距日十二度，有時得見，有時不得見。

　　一曰，氣清濁差如同是子正時，有時見極微之星，有時不得見四五等之星，氣則使之。其在月也亦然。

　　《論月體》

　　月體為圓球。何以知之？凡圓體於諸體中為最尊，如天、如日、月星、如地，亦於萬象中為最尊，故應圓，凡物之初體皆圓。〈如核如卵如胎〉諸大象，皆始造時之初體，故應圓。又月之體，半為明，半為魄。其明魄之界，時為弦直線，時為弧曲線。若果平體，何從得生弧線？且既為平面，日照之宜全體發光。如平面之鏡，一向日，即全鏡發光也。月為不然，則非平面○。試以人目居中，置一燭，東方稍遠置一球，西方稍近，相參直，即見球全受光。次不動目，燭獨移球西南隅，即見球大半為明、小半為魄。更移球正南，必明魄各半其界為直線。更移，得魄大明小。更移正東，必見全魄。燭為太陽，目為地、為人，球為太陰，以近遠日為光大小。其明魄界半周之間為直線者一而已，餘皆弧線也。

　　論其體質，非清非純，虛實雜也。故能映光不能透光，能發光不能迴光。何謂透光？如水，如玻璃、水晶、金剛石皆純清，故能透光。不止映光，非惟不能迴光，亦且不能發光。何謂迴光？如明鏡為全實，故能迴光。不止發光。非惟不能透光，亦且不能映光。月皆不然。而虛實、疏密，介在其間，故能映能發也○。然則何似稍似於雲。「雲掩日月，皆能映光，質薄則光顯，質厚則光微。

　　早日未出，夕日巳入，照雲成霞，霞照下土，虹霓之屬，本因雲氣而成光采，是為發光。體實則光大，體虛則光小。」月實似之，獨雲之映光多，發光少；月之映光少，發光多，此為異耳。

　　《論月駁》

　　月面不純一色，如斑駁然。昔人以為山河大地之景，不然也。山河大地之體，東西不等，云何月中之景時時不變乎？然則如何？此有二說

　　月駁圖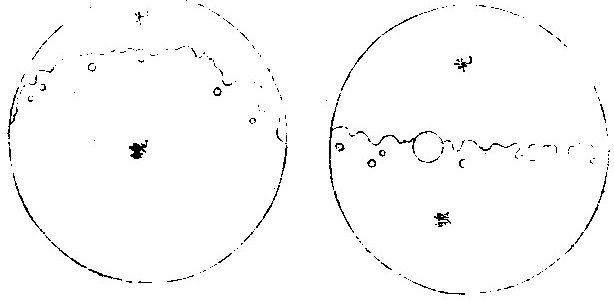

　　

　　月駁圖說

　　一曰：「月本圓體，特其體中疏、密、虛、實，不得純一，不能如鏡光合體，迴返所受之光，第因其本質所至，自為發光。密、實處發光大，虛、疏處發光微。」

　　如金剛石勝玻璃，玻璃勝水，其質疏密，虛實不等故。

　　「凡大光明中間有弱光，可指則曰大光中之駁點也；如大赤霞中間有淡紅，可指則曰大赤中之駁點也，是故名為月駁」也。一曰：月體如地球，實處如山谷土田，虛處如江海。日出先照高山，光甚顯，次及田谷江海，漸微，如人登大高山，視下土崇卑，其明昧互相容也。試用遠鏡窺月生明以後，初日見光，界外別有光明微點，如「海中島嶼然。」次日光長魄消。

　　日漸遠，明漸生，如人上山，漸遠漸見所未見。

　　則見初日之點，或合于大光，或較昨加大，或魄中更生他點。〈如日出地先照山顛次照平疇等〉「以光先後，知月面高卑」，此其徵已。

　　《論月光》

　　太陽為萬光之原本，其體至實。

　　光大小，因體虛實。如煉鐵之光，大于煉炭之光，鐵體實于炭也。

　　其質極純，〈質不純者光亦不純則不能大〉其體為「《全球》曲面。」

　　凡發光者，不論曲面直面，必須順平。若凹凸之面，不能發大光，稍有偏欹，光則相奪，亦不能大。

　　故在《大圜》中為「大光」之獨體，月及經緯諸星之光，皆從稟受焉。〈月借日光古語則然〉何以明之？如月食甚時，地球隔太陽之光，露光極微，目所難見，一也；日食甚時，月在日與人目之間，月之下魄不受日光，人目見之則為黑色，二也。

　　問：「月既無光，乃兩食甚時亦有淡光，此為何故？」曰：「體實無光，而能受光，而能發光。兩食之時，不受日光，而經緯諸星亦能映照，相受相發，因生微光矣。」

　　月光有二：一為對日而發光，名曰「正光」；一為日光不至，而從所受之處相映發為微光，名曰「次光。」

　　月受日光大半圖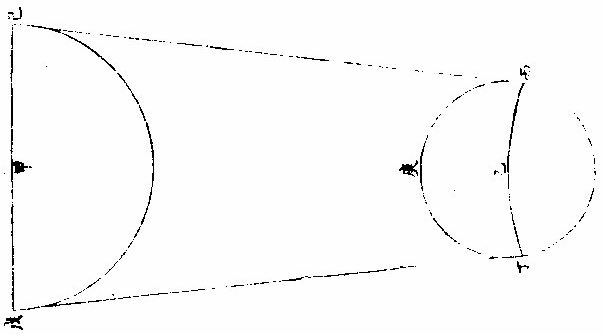

　　

　　《月受日光大半圖說》。

　　問：「月近日人見光小，遠日人見光大。何故？」曰：「月合朔時，外大半受光。」

　　「日體大，月體小」，則日必照月之大半。

　　人自下土止，視其內小半則無光，既而生明，所見漸大，至一象限則已見其受光之大半，故漸遠漸大也。

　　何謂日照月之大半？如圖甲為日，乙為月，戊丁己丙兩光線切月體，從丙從丁向乙，作兩垂線，成戊丁乙己丙乙兩直角，則丁乙乙丙兩線不成一直線。何者？凡一直線截平行兩線，其內兩角并與兩直角等，反之，若兩直線不平行，即一端漸近，一端漸遠，其漸近內兩角，必大于兩直角。今設丁丙兩直角，則丁乙乙丙不能以一直線與乙為角，若從乙心作徑線，必在丁丙兩點之上，則丁庚丙必月周之大半矣。

　　月近日受光之分大，遠日受光之分小。

　　月體自無運動，曷知之人所恆見，斑駁之象，終古不易。

　　月近日受光分大遠日受光分小圖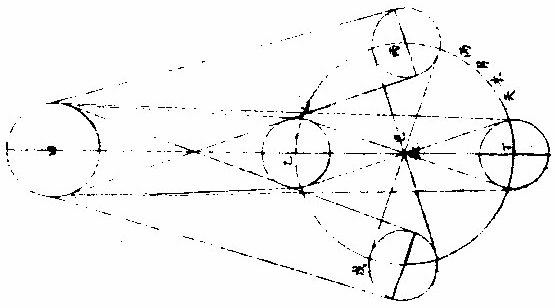

　　

　　《月近日受光分大遠日受光分小圖說》。

　　「月朔時，上大半為明，下小半為魄，月望時，上小半為魄，下大半為明」，兩弦各明魄半也。如圖甲為日，乙丙丁戊為月，本天人在地為己。月或上或下，恆半為明，半為魄，從人目作視線，自見月距日近光小，距日遠光大。

　　從「生明」以後漸長，生魄以後漸消，

　　人止見月體之小半，人目一點也。從點作兩線，切一圈，兩切線之內，弧必圈之小半。〈如圖〉

　　如上言，日照月得大半，人見月得小半，則定朢前後各數刻，月猶能發全光，滿大半之限，然後魄生而光減，非若晦朔之間，一瞬即生明也。

　　月去地有高卑人目所視有遠近圖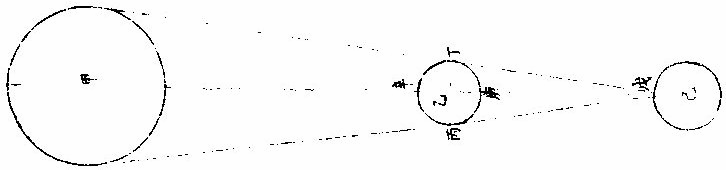

　　

　　月去地有高卑，人目所視有遠近《圖說》。

　　問：「日照月人見月各幾何數？」曰：「日月去地去人，各有高卑近遠不等。古法分月體周為三百六十度，折中推得日照月為一百八十一度六分度之一，人目見月為一百七十八度四分度之一，日照地為一百八十○度二十五分半。」

　　「月體地球」，其周分為三百六十度，與天等；

　　如圖甲為日，乙為月，己為地，日月之視徑約等。〈月在最高日在最高衝〉人目在戊，則戊丙戊丁兩視線，定見月之丙庚丁弧，從月心乙向丙向丁，作乙丙乙丁兩垂線，成乙丁戊丙斜方形，從乙戊平分之，作乙丁戊直角形。

　　形有丁戊乙角一十五分四十○秒。

　　日月視徑，並約為三十一分二十秒。

　　即丁乙戊角，必八十九度四十四分二十○秒，其丁庚為見月之半，弧倍之，得一百七十九度二十八分四十○秒。

　　若月徑為二十八分，則所見弧之小餘三十二分；若月徑為三十三分，則小餘二十七分。

　　因上圖推合朔時日照丙辛丁弧，丙辛丁者，丙庚丁之餘也，是為一百八十○度三十一分二十○秒。

　　用日距地之數及其比例，推得日照地為一百八十○度二十五分三十六秒。

　　月上下弦前後人所視有曲直線圖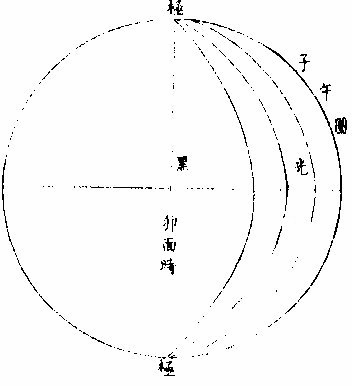

　　

　　月上下弦前後，人所視，有《曲直線圖說》。

　　問「月生明後，其光曲抱月體，至上弦下弦明魄之界則為直線，朢前朢後，明魄之界，又為弧曲之線，何故？」曰：「月本球體，人目所見，似為平面，其理正如平儀。然儀之子午圈，可當月周，皆大圈也。儀之極分交圈，可當上下弦，明魄之界，皆直線也。儀之時圈可當太陰。

　　每日距太陽漸長漸消，明魄之界，皆弧曲線也。凡儀」上大圈，皆分球為兩平分，其全見者獨子午圈耳。他諸圈皆半見半在儀之彼面，彼面者在月，則為上半球也。〈人所不見〉平儀曲線：〈即時線〉本是大圈斜絡於球，止見其半，故為不等。撱圈之半。

　　人視之為「撱圈」，漸消漸長，故不等。

　　月面《中明魄界》之弧曲線，本亦大圈，因其斜絡止見為半，亦不等撱圈之半也。

　　其與平儀本理未能全合者，儀上圈皆分球為兩平分。此依上言，月受光者大半，不受者小半，則明魄之照界別成一小圈，為大圈之距等，而非月球之中圈。

　　中圈必大圈也。分球為兩平分。人目所見之界，其直線則距等圈之似直線。〈本是圈也人視

　　為直〉其弧曲線，則亦距等撱圈之半也。以此之故，朔後三四日，新月之兩端，能過半周之界。

　　月光日所照與人所見時各不同圖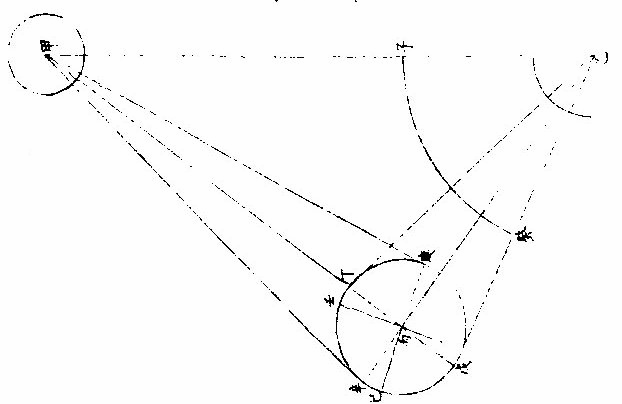

　　

　　月光日所照與人所見時《各不同圖說》。

　　問：「月行每日去離太陽約十二度等也。然朔前後光魄消長之分數少，兩弦前後消長之分數多，朢前後復少。人於定朢前後一二日見月光如不易，何故？」曰：「月禮本圓，圓面之上必有兩圈，皆為明魄之界，一為日所照之界，一為人所見之界，兩圈於定朔時相合為一。」〈照與見相反〉定朢時亦合為一。〈照與見相同〉過朔朢，漸相離。

　　如兩交圈結於兩極，漸展漸離相離之處，若黃赤二道之距遠度也。

　　兩界圈之距間，則人所見月體有光之分也。以此推之，人目所見為球之正面，如平儀之極分交圈也。兩界合圈，在球之側面，如平儀之子午圈也。初日相離距度若干，人側視之則見少；如時圈之近子午度分等，人側視之則見狹。兩弦時距度亦若干，人平視之則見多，如時圈之近極分圈度分等，人平視之則見廣也。故朔朢之消長非少而見少，兩弦之消長非多而見多也。如圖甲為日，乙為地，丙為月，丁丙戊庚為人所見月之半，己丙庚丁為日所照月之半，丁庚為兩界之距間，即本時人見月體有光之面也。

　　從目日及月心，作甲乙丙三角平面平分月體則己丁庚戊為圓面。

　　甲乙丙角形有甲乙。〈日距地心〉約一千二百地半，徑，有乙、丙。〈月距地心〉約六十地半徑，又有甲乙丙角，為月距日之度。〈試作癸子弧即得乙角之度〉求丙甲乙角設月距日之乙角，為四十度算，得一度五十五分，以并四十度，得四十一度五十五分。又引長乙丙戊，甲丙辛外角，即與丁丙庚角等。

　　庚丁壬丁壬辛，皆四分之一，各減共用之，丁壬，其兩餘等。

　　甲、丙辛外角與相對之兩內角等，即丁庚弧亦與兩內角等，則月距日四十度。人所見月體有光之分，約得四十二度。

　　言「約」者，未定之辭也。如上論月體明魄兩界圈似大圈，而實距等圈則有差。又約月距地為六十地半徑，然時多時少，日距地為一千二百地半徑，亦時多時少。又月經度距日四十度，或在南或在北，亦有差，是故約言之。

　　若測得月體明魄兩界之比例，可推月距日之度，即上《圖說》反用之。

　　每日月面光界圖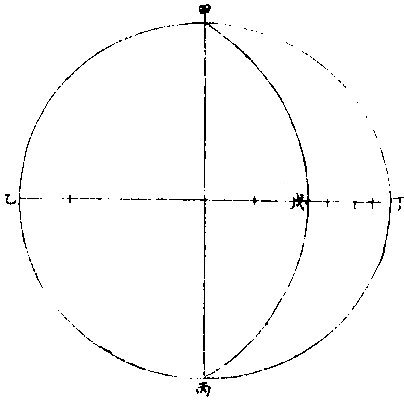

　　

　　每日月面《光界圖說》。

　　欲圖某日之月光界，先求月距太陽若干度分，次依上法求月面半徑上明魄界若干度分，從兩極。

　　月面上兩極定為過白道，兩極之大圈線，或與白道為直角。

　　作撱圈之半，乃本日所見月面有光之界也。若未至九十度，光作角形，若過九十度，作未成圓形。如圖甲丙為月之兩極，丁戊為明魄之界，甲戊丙線為本日之月光界，甲戊丙丁為兩角之形，甲戊丙乙為未成圓形。

　　用上法推凡日光界為全徑。

　　十分之一，距日二十六度；

　　十分之二，距日四十度半。

　　十分之三，距日六十度；

　　十分之四，距日七十二度半。

　　十分之五，距日九十度弦也；

　　十分之六，距日一百○七度半。

　　十分之七，距日一百二十度；

　　十分之八，距日一百三十五度半。

　　十分之九，距日一百五十四度。

　　滿十分距日一百八十度，朢也。

　　以上數依《目測》為定。若推算當求月高卑，求白道緯度，當有微差。

　　月朢光色中邊有淺深圖

　　

　　《月朢光色中邊有淺深圖》說。

　　問：「月朢時，中心光色稍淺，四周光色特深，何故？」曰：「月體圓，中心體一分發光一分，四周體三分發光一分。

　　一分者，所受日光少，故發光淺；三分者，所受日光多，故發光深。」如圖甲為月體，乙為目，見月之角，從角分為十分，中一分見月周一十一度有奇，旁一分見月周二十五度有奇。

　　《曆象圖說》

　　太陰次輪圖四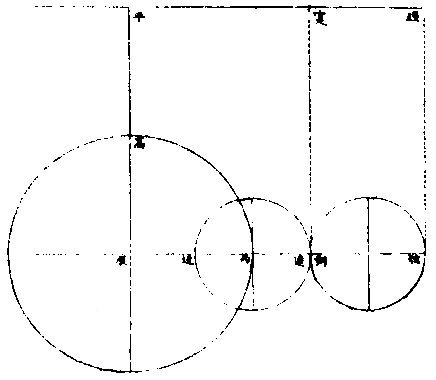

　　

　　太陰次輪圖二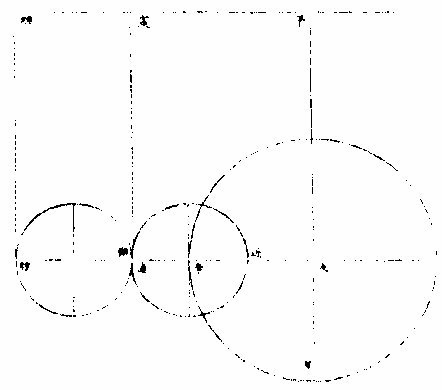

　　

　　太陰次輪圖三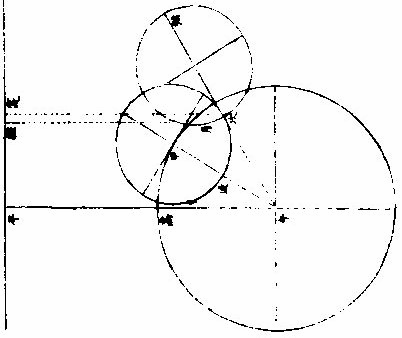

　　

　　太陰次輪圖一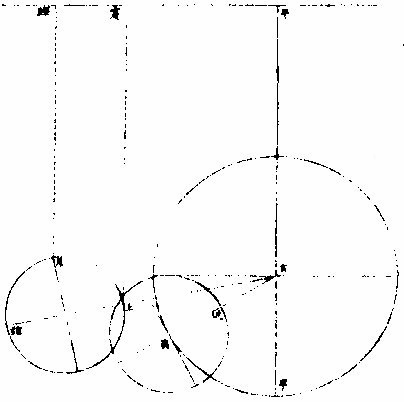

　　

　　太陰次輪圖說

　　「均輪之心行于本天，小輪之心行于均輪」，此各曜之所同也。乃各曬光體又行于次輪，而次輪之心行于小輪。惟太陰繫于小輪而行者，不以次輪之心，而以次輪之邊，故其遲疾加減，與各曜有不同者。次輪起于距日之遠近，亦各曜之所同也。乃五星之次輪，木火土與日一合而行一周，金水與日再合而行一周。

　　惟太陰次輪與日一合而行再周，故其遲疾加減，與各曜尤有不同者。次輪邊界從合朔起，繫于小輪為最近，半周上弦而至遠矣。一周復於近為朢，又半周下弦而遠，再周復於近而合朔矣。次輪以此朔朢點繫於小輪上右轉，周行既倍於小輪心行於均輪之度，而月體之行於次輪周者，又一合「朔而有再周。」由是均輪既有高卑，小輪又有遠近，次輪上復有朔朢二弦，而太陰之所在，測其經度而有遲疾，測其緯度而有出入，測其光體周徑而有益損，象數可徵，皆古法之所未備。如《一圖》均輪心行至辰，小輪心自高行至丙，各一象限。次輪朔朢點必自近至遠，行一百八十度，其平實之差為一均數，若月在次輪弦點，則更有《實經》之差。〈二三均〉當并於「一均，為極大之減均」也。〈古名遲疾差〉二圖均輪心行至戌，小輪心自卑行至辛，各一象限。次輪朔朢點必自近至遠，行一百八十度，其平實之差，為一均數。若月在次輪弦點，則更有實經之差，當并於一均為極大之加均也。〈古名疾差〉三圖均輪心行至午，小輪心自高行至甲，各三十度。〈朒初限〉次輪朔朢點在小輪上，必自近至次行六十度。其平實之差，為一均數。若月在次輪，自次向弦行至月，則有實經之差，當損其一均。餘平經之差，為定減均也。四圖均輪心行至亥，小輪心自卑行至庚，各六十度。〈脁初限〉次輪朔朢點在小輪上，必自近至上行一百二十度，其平實之差，為一均數。若月在次輪，自上行至月，則有實經之差，當益其一均，得平經之差，為定加均也。

　　晦朔弦朢圖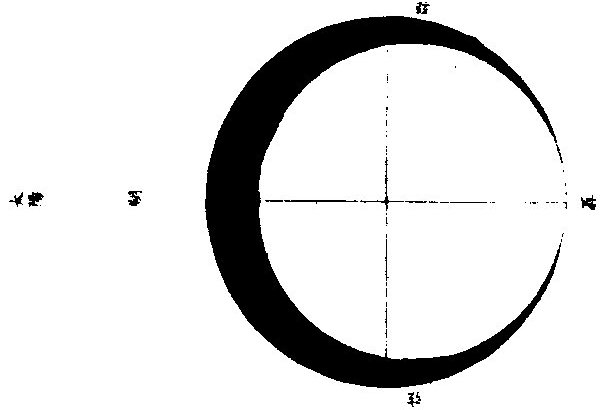

　　

　　晦朔弦朢圖說

　　月借日光，故與日同度，則人見其相合而晦。自朔後漸遠於日，而生明。與日近一遠三，則半明半晦為上弦，與日對度，則全體皆明，為朢。自此漸追及日而生魄。迨與日遠三近一，又半明晦為下弦。及再追及日而與之合度，則又一晦明矣。

　　《曆象圖說舊本》

　　月道交周圖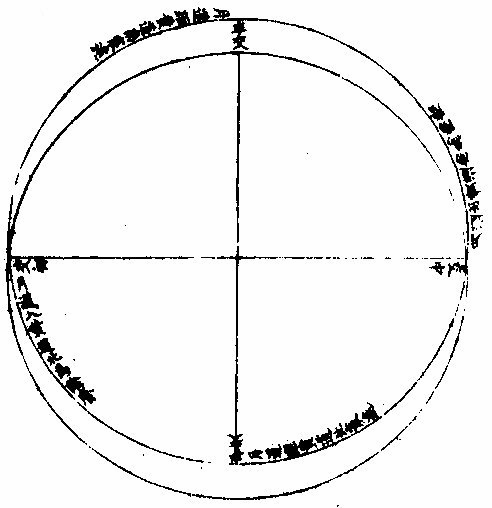

　　

　　月道交周圖說

　　月道斜交黃道，交初入黃道北至交半緯度極大，乃向黃道行至交中，出黃道南極，於交半緯度又最大，又向黃道行至交初，而一周，每周退天之度為交差○。《黃鐘曆議》云：「今書傳官本，有圖為圜規者九，而重疊相錯，先儒所傳九道蓋如此。以理究之，月道如今纏線於彈丸上，線道雖重，然止一縷往來，未嘗斷絕。

　　果」如九規，則斷而不相屬。此可見九行之說非也。每一交之終，退天一度，餘凡二百四十九交有奇，退天一周，終而復始，故舊《曆》所謂九道元人一之，名曰白道○。鄭世子以月道出入黃道之差，譬黃道交於赤道之差，其說已當。然以今曆之理揆之，則月道之交差者，月退也；黃道之交差者，恆星進也；而「日度不移」，此其所異也。月之為體最近，其行度最著，故推日星之理者自月始。由其交周，可知天日之有歲差矣；由其遲疾，可知日星之有盈縮矣；由其月孛之行，可知日最高之有移度矣；由其倍離合日，而又有遲疾加減之分，可知五星之有歲輪矣。

　　太陰次輪圖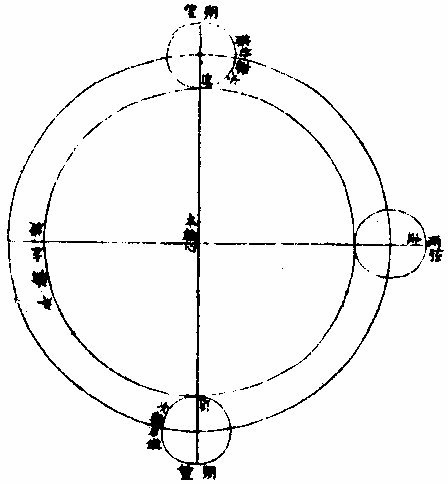

　　

　　太陰次輪圖說

　　「五星皆以次輪心行於本輪之周，月則以次輪最近。」點行於本輪之周，朔朢起最近。每本輪心離日一度，則次輪最近。行於本輪周亦一度，而月在次輪則行兩度。朔朢至弦，離日九十度，而月行次輪一百八十度，至最遠。弦至朔朢，亦行一百八十度，復至最近，故一月行兩周。〈所以知者高卑視徑遲疾視行皆至兩弦則其差倍增而朔朢則平也〉

　　太陰高卑四限圖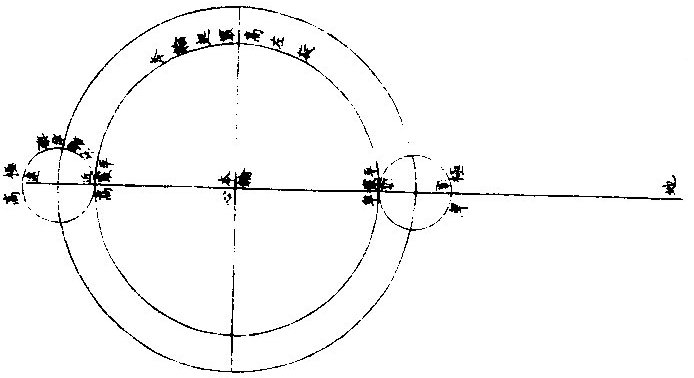

　　

　　《太陰高卑四限圖說》：

　　本輪最高，又遇次輪最遠，為極高本輪最高；遇次輪最近，為次高本輪最卑，遇次輪最近，為次卑本輪最卑，又遇次輪最遠，為極卑。高則去地遠，視徑小；卑則去地近，視徑大。

　　太陰遲疾大差圖〈亦分四限〉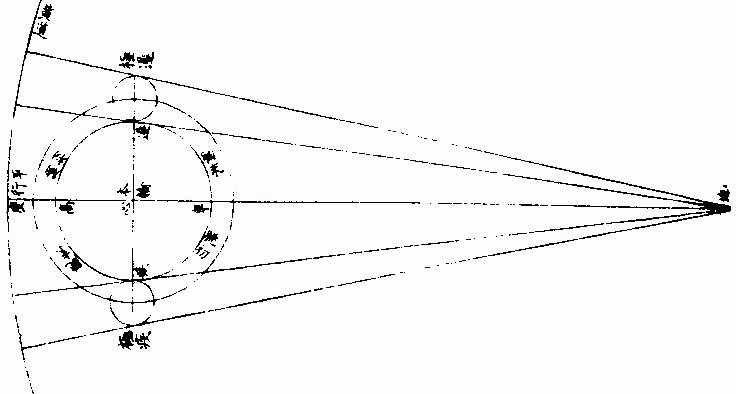
　　

　　《太陰遲疾大差圖說》：

　　自本輪最高行滿朒初九十度至留際遲積度，五度奇。自最卑行滿脁初九十度至留際疾積度，亦五度奇，是為本輪上遲疾大差，朔朢用之。若本輪行至留際，又遇次輪之最遠，則其遲疾各得七度四十分，以為大差。兩弦用之。是為遲疾大差之四限。

　　闇虛蝕限圖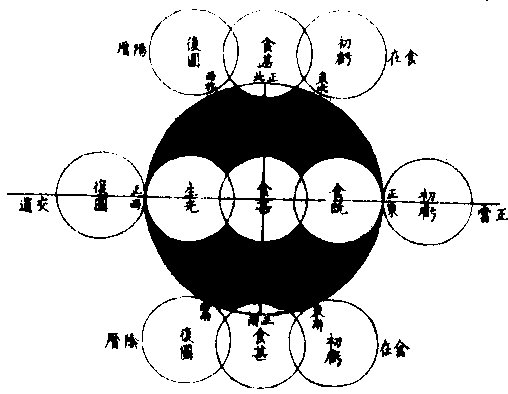

　　

　　闇虛蝕限圖說

　　闇虛徑大於月，約將三倍。又各以去日遠近為大小正當交道，則蝕有五限。〈月東輪切闇虛西輪為初虧西輪齊為食既中徑齊為食甚東輪齊為生光月西輪切闇虛東輪為復圓〉偏而蝕於陰陽者，分三限。〈初虧食甚復圓〉起復方位，與「日蝕反。」〈日遲而月來揜之故起於西闇虛遲而月來就揜故起於東〉緯度多則蝕分少，緯度少則蝕分多○。古人指日中之暗為闇虛。鮑雲龍《天原發微》，比於離坎中之陰陽。宋濂謂月蝕為地影之所隔。魏文魁作《曆測》，疑其說出於西域，然《南齊書》已言之。且漢張衡亦曰：「當日之衝光常不合者，蔽於地也，是謂闇虛。」斯言甚明。

　　獨以為在星星微，與今說異。月近地，星遠地，日照地成影，闇虛有盡，不能及星也。

　　里差時刻圖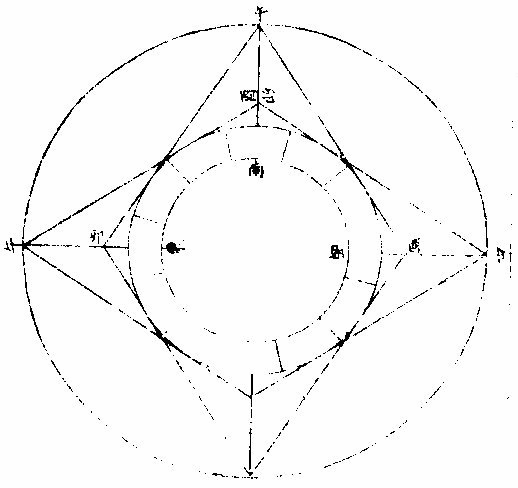

　　

　　里差時刻圖說

　　北極高下殊，而地有南北之緯差；時刻早晚異，而地有東西之經差。測經差時刻者，用月蝕。月蝕普天同見而見之者，西方覺早，東方覺遲。知相距幾何里，即差幾何刻，則推之四表，莫不皆然。蓋東之午南視為卯；南之午西視為卯，而東巳視為酉；西之午南視為酉，而東必以為子。各據日輪南照為午，而在左在右，初不知時刻之潛移也○。《堯典》「分宅四方」，《周官》以日南、日北、日東、日西，參互測驗，誠曆象之至要。後世率就一隅立法，故用之他方，隔閡難通也。耶律楚材創里差法，郭守敬廢而不用。雖分道測候，而所定授時僅可行於大都，元統強以用之，江南止改其晝夜刻，疏謬已甚。其後都北平，臺官一守元統之舊，又襲南方之晷漏而不知變，曆象之難明也如此。

梦远书城(guxuo.com)