古今圖書集成·乾象典第三十二卷

第三十二卷

　　日部彙考

　　《易經》

　　《說卦傳》

　　離為火、為日。

　　〈大全〉節齋蔡氏曰：「內暗外明」者，火與日也。離內陰外陽，故「為火為日。」

　　《禮記》

　　《月令》

　　孟春之月，日在營室。

　　〈注〉「日月會於諏訾」，而斗建寅之辰也。〈陳注〉營室在亥，諏訾之次。

　　仲春之月日在奎。

　　〈陳注〉奎在戌，降婁之次。

　　季春之月日在胃。

　　〈陳注〉胃在酉，大梁之次。

　　孟夏之月，日在畢。

　　〈陳注〉畢在申《實沈》之次。

　　仲夏之月，日在東井。

　　〈陳注〉東井在未，鶉首之次。

　　季夏之月，日在柳。

　　〈陳注〉柳：在午，鶉火之次。

　　孟秋之月，日在翼。

　　〈陳注〉翼在巳，鶉尾之次。

　　仲秋之月日在角。

　　〈陳注〉角在辰，壽星之次。

　　季秋之月日在房。

　　〈陳注〉房在卯，大火之次。

　　孟冬之月日在尾，

　　〈陳注〉尾在寅，《析木》之次。

　　仲冬之月日在斗。

　　〈陳注〉斗在丑星紀之次。

　　季冬之月，日在婺，

　　〈陳注〉女在子《元枵》之次。

　　《爾雅》

　　《釋地》

　　觚竹、北户、西王母、日下，謂之「四荒。」

　　〈注〉《觚竹》在北，《北户》在南，《西王母》在西，《日下》在東。〈疏〉北户者，即日南郡是也。顏師古曰：「言其在日之南，所謂北户以向日者。日下者，謂日所出處，其下之國也。」

　　又

　　《岠》齊州以南，戴日為丹穴。

　　〈疏〉戴，值也。言去中國以南，北户以北，值日之下，其處名丹穴。

　　又

　　東至日所出為《太平》，西至日所入為《大蒙》。

　　〈疏〉即《淮南子》云「日出扶桑，入于蒙汜」是也。

　　《書緯》

　　《考靈曜》

　　仲春仲秋，日出于卯，入于酉。仲夏日出于寅，入于戌。

　　仲冬，日出于辰，入于申。日光照四十萬六千里。

　　《淮南子》

　　《天文訓》

　　「日。出於暘谷。浴於咸池，拂於扶桑，是謂晨明。登於扶

　　桑之上，爰始將行，是謂胐明；至于曲阿，是謂旦明；臨于曾泉，是謂蚤食；次于桑野，是謂晏食。臻于衡陽，是謂禺中；對于昆吾，是謂正中。靡于鳥次，是謂小還；至于悲谷，是謂晡時。迴于女紀，是謂大還。經于虞淵，是謂高春；頓于連石，是謂下春。爰止羲和，爰息六螭，是」謂懸車。薄于虞淵，是謂黃昏；淪于蒙谷，是謂定昏。日入崦嵫，經于細柳。入虞淵之汜，𥌓于蒙谷之浦。日西垂，景在樹端，謂之桑榆。行九州七舍，有五億萬七千三百九里。

　　《魏張揖廣雅》

　　《日》

　　日名「曜靈」，一名「朱明」，一名「東君」，一名「大明」，一名「陽烏。」初出為旭，日昕曰晞，日溫曰煦。日在午曰亭午，在未曰昳，日晚曰旰，日將落曰晡，又曰薄暮。日光曰景，日景曰晷，日氣曰睍。日西落光反照于東，謂之反景。在上曰反景，在下曰倒景。日初出曰朝暾，曰寅賓，日斜曰暆，日御曰羲和。

　　《吳徐整長曆》

　　《日徑》

　　「眾陽之精」，上合為日，徑千里，周圍三千里，下于天，七千里。

　　《晉書》

　　《天文志》

　　日為太陽之精，主生養恩德，人君之象也。

　　《刻漏經》

　　《定太陽出沒法》

　　正月出乙入庚方，二八出兔入雞場，三七發甲入辛地，四六生寅入犬藏，五月生艮歸乾上，仲冬出巽入坤方，惟有十與十二月，出辰入申仔細詳。

　　《隋書》

　　《天文志》

　　「日循黃道東行，一日一夜，行一度三百六十五日有奇而周天。」行東陸謂之春，行南陸謂之夏，行西陸謂之秋，行北陸謂之「冬行」，以成陰陽寒暑之節。

　　《明陽瑪諾天問略》

　　《日天本動及日距赤道度分問答》

　　「赤道則第十一重宗動，天之分中也。周天三百六十度，去南極九十度，去北極亦九十度，為赤道，所謂天之中。而其南北二極，天之極也。黃道則第四重日，天之分中也。周天三百六十度，南北亦各距九十度，為黃道，所謂日，天之中也。日天本動，自西而東，其南北二極，離宗動天，赤道之極二十三度半，黃道以南，以」北，離赤道二十三度半，為冬夏至；黃道以東以西，與赤道相交，為春秋分。

　　黃赤道二分二至圖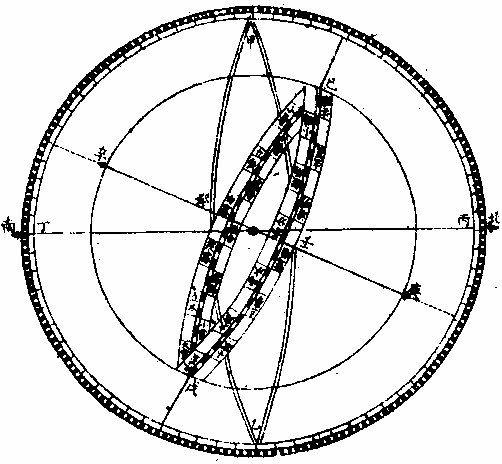

　　

　　黃赤道二分二至圖說

　　如右圖甲乙為赤道宗，動天之中，丙丁為赤道南北二極，己戊為黃道日。天之中，庚辛為黃道南北二極，日天庚辛二極離宗，動天丙丁二極各二十三度半，日天己戊黃道離宗，動天甲乙赤道二十三度半，而為冬夏至黃道赤道相交於壬癸，而為春秋分宗，動天自東而西，一日一周，因而帶動。其下十重諸天，亦自東而西，一日一周日，一日約行一度，一歲一周。故自戊冬至至壬春分，為九十度。九十日自壬春分至己夏至，自己夏至至癸秋分，自癸秋分至戊冬至，亦然。略論三百六十五日有奇，一周天也。《宗動》天自東而西，一日一周，即此周日之間。日之自西而東，自行一度，人只見其自東而西，左旋而已，初不見其右行者，何也？以其外動之自東而西者甚疾，內動之自西而東者甚遲故也。然而因其近遠天頂可以證之。春分以後，日過赤道北而上，秋分以後，日過赤道南而下。其上其下非日有偏行，緣與宗動天不同極耳。試看上圖，庚辛為日天之極。若日輪在戊，冬至以至壬，春分漸上以至己，夏至亦上過己夏至，至癸秋分即下至戊冬至亦下。上下由於本天之極，原離赤道之極二十三度半，故日輪居本天之中，亦離赤道南北二十三度半，而春秋分必相交。乃知氣不參差無以成化，時不寒暑無以合序，物不錯雜無以生文。

　　儻日天二極與宗動天同，則日動恆在赤道下，絕無距度，安得有東西運行之異。以行變化。而稱貞觀貞明之體哉。

　　日輪正居日天之中，日天動而日輪亦動，日天運行之一周，如《於宗》動天畫一道焉，所謂黃道也，終古如是。故日輪恆躔黃道一道，不出入於南北界，非如月、五星之出入於十二度內也。其上下四時，各有定度，不稍前後也。黃道周天三百六十度，分為四分，每分九十度為四象限。又一象限分六分，每分十五度為一節氣，共二十四節氣。

　　日輪遠近分寒暑圖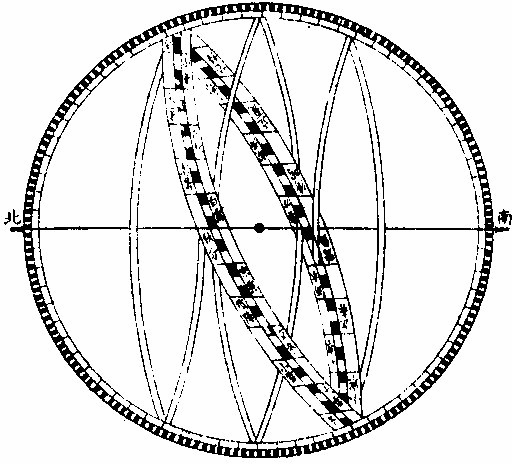

　　

　　《日輪遠近分寒暑圖說》。

　　如右圖。「自冬至至春分，則周天象限也，分得九十度，每節氣十五度，則六節氣也。自春分至夏至，自夏至至秋分，自秋分至冬至，亦然。日輪躔冬至初度至九十度，在赤道外而最遠於天頂，故自立冬至立春皆寒，而冬至在其九十度之中，故其寒尤甚。自立春至立夏，因日漸近赤道而稍近於天頂，故其時暖於冬至，涼於夏至，正交赤道，謂春分也。自立夏至立秋，因日在赤道上，而夏至則最近於天頂，故其時甚熱。自立秋至立冬，日漸下而離天頂，其時稍冷，於夏至，甚暖於春分，亦交赤道，所謂秋分也。」夫春秋分皆躔二道之交，其離天頂同，則其成寒暑宜亦同。緣春日陰氣塞滿大地，日光雖照，難成溫熱；秋日陽氣焦灼。無所不暴。日輪雖下，難成寒氣。故春秋二季，日離天頂。

　　並同而寒暑不同也。

　　「日。自春分至夏至，行九十度為六節氣。自夏至至秋分亦然。」《四象限》雖各行九十度，而其距赤道之緯度則非九十度，游移不出二十三度半也。故九十度為黃道自東而西之度數，而二十三度半為黃道距赤道南北之度數也。蓋春秋分日，日躔二道之交，過春分日離赤道向夏至而漸遠赤道，過此則又漸近赤道矣。自秋分至冬至、自冬至至春分，亦然。

　　二十四氣日輪距赤道遠近圖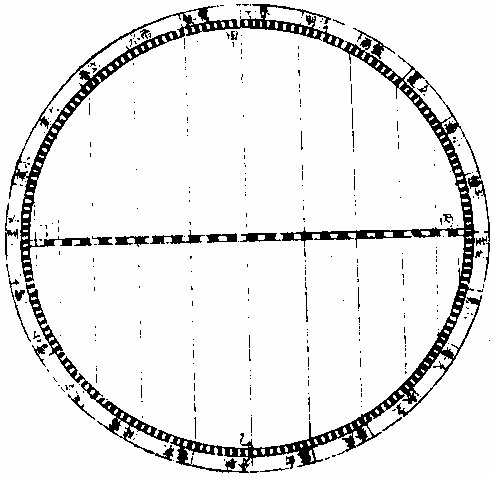

　　

　　二十四氣日《輪距赤道遠近圖說》

　　如右圖，甲乙為赤道，丙丁為冬夏二至，距赤道二十三度半。假如日輪在春分，則於赤道無距度，自春分至清明，則日行十五度，而其距度非十五度，乃六度十九分也。自立夏至小滿，此十五日之間，其遠非六度，而為四度也。自芒種至夏至，亦非四度，而為一度弱也。故近交差多，近至差少，而其差非同也。欲知每節氣及每日日躔，黃道距赤道幾何度分，依上《圖》可得焉。假如清明初日日距赤道度分，上是清明初度，下是白露初度，兩界相對，次用一線或界尺隱取兩界，循直線視所當丙丁線度分，得六度，因知清明白露初日日距赤道六度也。又清明五日、處暑十日，其離甲乙赤道亦同。故撿取清明五度、處暑十度，為兩界次。依法視於丙丁，得七度強，即其距度也。餘倣此。

　　《日蝕問答》

　　問日蝕所以。曰：「日蝕，非日失其光，乃月掩其光也。月之天在日天之下，朔時月輪正過日輪之下，南北同經，東西同緯，故掩其光，若有失之耳。」

　　月正當日下見食圖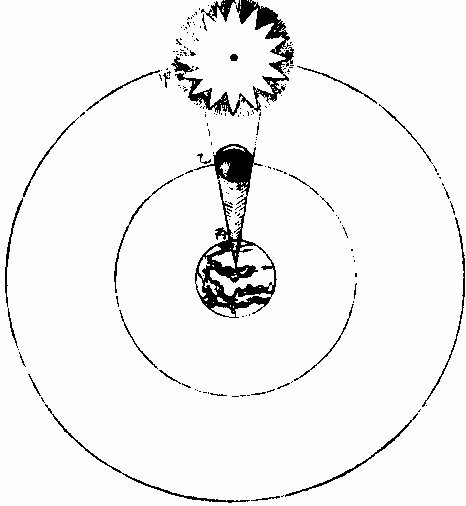

　　

　　月正當日，下見《食圖說》。

　　如右圖，甲為日，乙為月，丙為人，居地面，月輪隔在其中，使日光不能照地面，而人目不能見日輪也。因知日食非各處共有之，或一處見食，別處見光，或一處全食，別處半食，皆目隨地異也。聞貴國先時一年日食，司天言「當幾分，草澤言當幾分」，後卒如草澤言，說者以為算法疏密使然，實不爾也。

　　月不正當日下不盡見食圖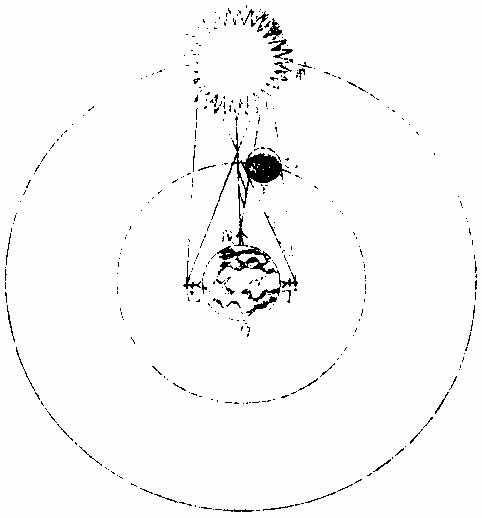

　　

　　「月不正當日下不盡」，見《食圖說》。

　　如右圖。丙地面，乙月輪，甲日輪。居丁者正，見月于日，故見全食；居戊者斜，見月于日，故見半日食；居己者不，見月于日，故全不見食。如欲得日食時刻最準，先須得七政經緯度及正斜視法。不然，即交食分數，測驗躔度，悉不可算，悉不可定。故吾國曆家窮究此理，以為曆準，別有備論，今特略言食理也。試觀居房內者，房中有燭，以照四方。若于東方有掩光者，必坐東者不見其光，而坐南北西方者得光也。各方如是，如滅其光，則居諸方內者，四方見燭無光矣，與食同理也。若月食，則所食全缺分秒，萬人萬目，共作是觀，別無同異，與日不同。

　　問：「日蝕由于月掩其光。凡每朔時，日月同度，又正過其下，宜皆得食。今不盡然，何也？」曰：「日躔惟一黃道，終古無出其外也。月于黃道，有時在南、在北，故月道半出黃道北，半出黃道南，而為南北二交，吾國所謂龍頭龍尾是也。朔時若月在二交之外，或南或北，與日非經緯同度，不能揜日光也。南北為經，東西為緯，凡」是朔日，經度必同；如更同緯度，適在二交之上，乃能揜其光而食耳。

　　日月同經度不同緯度不食圖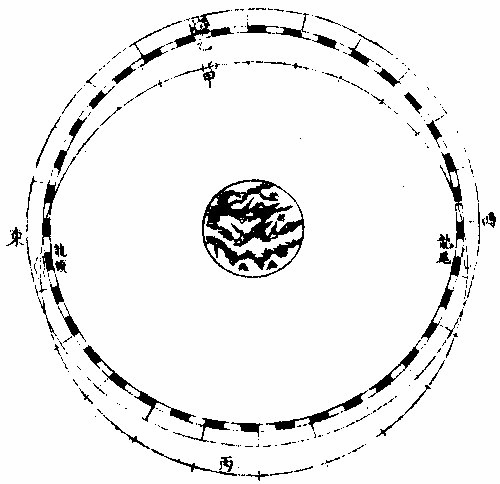

　　

　　《日月同經度不同緯度不食圖說》：

　　如右圖，月道交黃道于龍頭龍尾。甲為月道，在黃道南，丙在北。試使月朔時在龍頭，則經緯同度，月正過日輪之下，揜其光而食焉。如朔時月在甲黃道之南，日乃在乙黃道之上，而緯不同度，則日在北，月在南矣，故「不食」也。

　　問：「日食，若因月天在日天之下，則水星、金星天亦在日天之下而不見，揜其光？月天在金水二星之下，月亦宜揜其光，而金水有食如日矣。今其食不顯，何也？」曰：「水星、金星雖正過日輪之下，而有與日同度時，然金星大于水星，而日大于金星一百倍。二星之體比日體甚小，豈能揜其光而使人不見日也？吾國曆家」遇金、水二星與日同度，恆見日輪中有黑點，以星體不能全揜日體故也。月輪正過二星之下，亦宜揜其星光，使人不見。今不顯其食如日者，非月不能揜之，乃二星之光甚微，其體甚小，故不明顯也。

　　問《天地渾儀說》曰：「地球大于金星三十六倍又二十七分之一，大于月輪三十八倍又三分之一，是金星大于月輪也。夫月輪能揜日光，則金星更大，亦何不揜日光乎？」曰：「凡物以形相揜，非惟論其大小，又當計其遠近。蓋人目視物之時，自目至物之體，射兩直線為直角形。故愈近于目，其物雖小而徑愈大；愈遠于目」，其物雖大而徑愈小

　　金星在月上不揜日光圖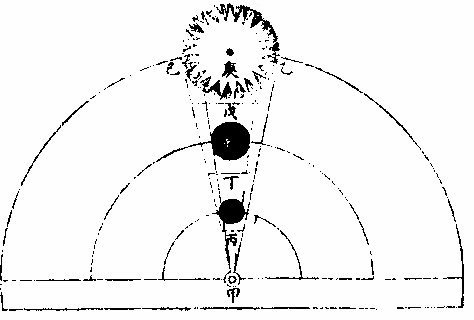

　　

　　金星在月上不揜《日光圖說》。

　　如右圖，甲為人目，庚為物體，甲乙甲己為人目，所射兩直線，則徑愈近愈小，愈遠愈大，故「戊大于丁，而丁大于丙也。」試以人手隔目，手愈近于目，則愈揜物體矣。是故金星雖大于月，乃在月天之上，去人目甚遠，故不能揜日光也。月雖小于金星，乃在金星天之下，去人目最近，故能揜日光也。此其理也。

　　問：「日大於月固矣，日輪較地球不知其大有幾？」曰：「吾國曆家著明此理，有論甚廣。測七政高下及大小之度分，有器甚準。日大于地，一百六十五倍又八分之三。欲徵之，宜知圓光照圓體之影也。圓光若照圓體同大，其影廣恆等而無窮。若照圓體更大，其影漸大，而亦無窮。若照圓體更小，其影漸小，而有盡。」

　　日輪大于地光影漸小圖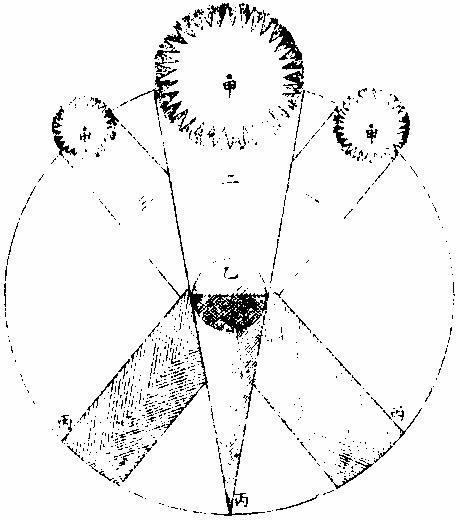

　　

　　「日輪大于地光影漸小」《圖說》。

　　試觀右圖，甲為圓光，乙為圓體，丙為體影。第一圖，甲圓與乙圓體相等，丙影亦等，無窮盡矣。第二圖甲圓光大於乙圓體，丙影漸小而有盡矣。第三圖甲圓光小於乙圓體，丙影漸寬大，而亦無窮矣。太陽照地之時，地影非恆等，亦非漸大。譬之物影，其為漸小而有盡。如第二圖也，則以日輪圓光大於地形也，地之影漸銳而小，至有盡焉，甚明也。凡星月無光，借日之光，太陽照及其體，則光生焉，不然則否。儻日與地等，地或更大焉，則其影為無窮之影，宜射蔭直過諸星之天，必見諸星有食焉者矣。今惟地體甚小，銳，影有盡不到諸星之天，故日光無礙照及木火土，以及列宿諸天，而諸星恆明，光無朦也。其地影之盡，可過第一、第二重天，至第三重天，而不及第四重天，所以月因地影得食，而諸星不食也。地球一周三百六十度，每度二百五十里；日天一周亦三百六十度，其每一度有數萬餘里焉。吾國曆家有器量得日天之度，每半度為日一全徑，因知其圓形亦得數萬餘里，而非地形可比。譬如山高二十餘里，上有人焉，居下者視之如小鳥也。日天之高，自地面至太陽中心，相隔一千六百萬餘里，今視日輪如小車輪，猶之二十里高山，視人如鳥矣。

　　問：「太陽早晚出入時近於地平見大，午時近於天頂見小，何也？」曰：「地球懸於空際，居中無著，其四際離天，諸方同一，無近遠也。以理論之，其在東西出入方也，太陽離地凡一千六百萬餘里矣。而人立地面，或自東視西，或自西視東，半徑幾一萬五千里焉。以一千六百萬餘里，又加以一萬五千里，人之視日宜小也。

　　日在午方，從下視上，止一千六百萬餘里，人之視日宜大也。今宜小而反大，宜大而反小者，此非由于地之遠近也，濕氣使然也。蓋夜中水氣恆上騰，氣行空中，悉成濕性。濕以太陽自下而上，映帶而來，晃漾焉，蓬勃焉，人望之以為如是其大耳。若太陽當空，浮翳盡掃，無所映隔，真體明淨，較之旦暮」為小。凡月與諸星見于地平，必有濕氣障隔，爾時所見，亦必大于午時。試觀水中所見，或石或木，必大于水外者，皆濕性之勢也。

　　問：「人在地面，視東視西者，半徑各得一萬五千里，豈以人之所立，恰在地中乎？」曰：「地是圓體，人之所立，無論遠近中邊，從其所立分之，各得一半。」

　　《晝夜時刻隨北極出地各有長短問答》

　　問：「晝夜長短不一，時刻亦異，何也？」曰：「晝夜長短，由于太陽及南北極出入地平也。北極出地即夏至晝長夜短，冬至晝短夜長，南極出地反是，其時勢異也。為此夏至，為彼冬至，故晝短夜長；為此冬至、為彼夏至故晝長夜短。南北二極與地平，則其地晝夜恆平，故晝夜長短，由於太陽及極出入地也。南北為緯度，東西為經度，各一周三百六十度。人在地面，凡居經度一帶之內者，其晝夜長短恆同，其日出入及晝夜時刻則異。」蓋經度之自東而西者，人之所居，或東或西，雖各不同，而緯度之三十度者皆為三十度，四十度者皆為四十度也，此同緯度者也。若緯度之異者，自赤道以至極下，其晝夜長短各異矣。

　　人居地四圍各以天頂日輪為時早晚圖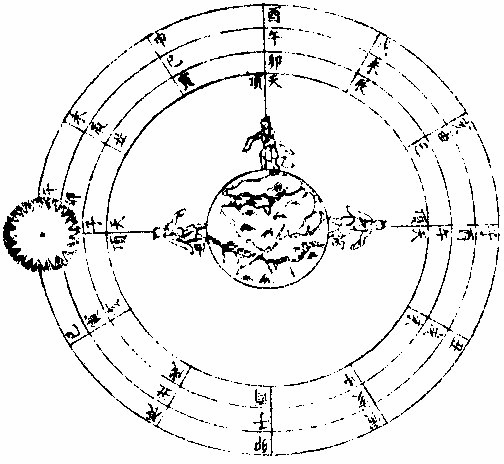

　　

　　人居地四圍，各以天頂日輪為時，《早晚圖說》。

　　如右圖。地為圓體，懸於空際，上下四旁皆有人居。四方之人各以所居子午線為午時，太陽在東方。甲居東方者為午時，日輪在其天頂故也；乙居西方者即為卯時，日輪至天頂須三時故也；丙亦居西方者即為子時，以日輪至天頂須六時故也。諸地相去，自東而西，莫不皆然。地球自南而北，三百六十度一周；每「一度二百五十里。日輪每刻平行天度三度四十五分。」如兩地相去九百三十七里半，則相隔為一刻；相去七千五百里，則相隔為一時。因知居東方者，若得午時，自此逐漸往西，即為巳、為辰、為卯、為寅、為丑、為子。天下自東而西，時刻各異，各以日輪到本處子午線為午正初刻。晝夜長短恆同者，蓋以北極出地多寡定為時刻多少，所以自東而西一帶；但經度相同地方，其離北極皆同，則晝夜長短亦同。

　　《羅雅谷日躔曆指》

　　《春秋雨分時太陽之本度》

　　曆法家古來有公論二端，其一曰：凡動而有怯者三：一、自上而下，如土石等重物，以地心為界。〈為界者欲至地心而止〉二、自下而上，如氣火等輕物，以月天為界。此二動自行必成直線，名為「直動」；三循環行一周至元界，如天行一周成全圈，名為「周動」也。三者而外，皆名無法之動。

　　其二曰：「凡天體及七政恆星等，必平行不平行，則推步之術，無從可立，無從可用矣。然而人目所見，各有遲疾順逆，時時遷革，百千萬年，無一平行者，又何也？曆家因此推求，悟有不同心之圈及諸小輪等，雖有彼此前後多互異之說。總之欲得其不平行之故，而又不失其平行之恆理，不得不然耳。」

　　太陽之公動，其理不一，如屬宗動天，而定晝夜之時之類。今略論其本行，曰：「太陽既為周動，又必平行，則人目所見，經歷歲月日時，悉宜平等。」則從天正春分至秋分，又從秋分至春分，平分一歲，其日亦宜平等。

　　乃從春分晝夜平至秋分，歷一百八十六日有奇而平；從秋分晝夜平至者，分歷一百七十八日有奇而「平所差八日有奇，安得謂之平行？」又「人目所見太陽之體，冬至則大，夏至則小，見大去人必近，見小去人必遠。」又冬至月食，小於夏至之食。蓋大光之體愈遠，其景愈長愈大，月過地景之時愈多，故知時多者景大，景大則光體必遠。既兩有冬夏遠近，又安得謂之周動？且漸遲漸速，漸大漸小，非驟然遷變，即又日日刻刻皆非平行也。今欲明遲速之故，而又不失其平行，欲明大小之故，而又不失其周動，將何說以處於此？

　　太陽本行圖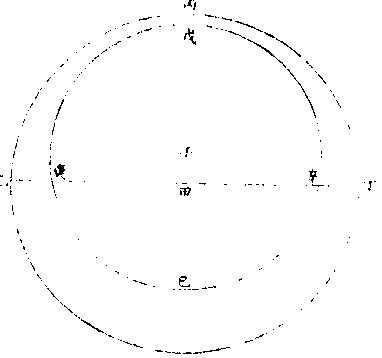

　　

　　太陽本行圖說

　　如圖甲為地心，乙丙丁為宗動天，庚己辛戊為日輪本天，庚辛為春秋兩分，戊己為冬夏兩至。若兩圈為同心者，即庚戊辛半周，辛己庚半周，所得圈分必等。

　　今不等，必緣不同心，故人目不在太陽本天之心壬，而在宗動天之心甲，則日行本輪，天恆平行，而人目所見者，庚戊辛所經之日，多於辛己，庚所以冬縮而夏贏也。日在戊，去甲遠，在己去甲近，故「冬大而夏小」也

　　《鄧玉函測天約說》

　　《太陽篇從本體論》

　　論「太陽之形象，本是圓體○，圓有面有體。太陽之為圓，而舉目即是，不待言矣。其為圓體，何從知之？」曰：「凡物未有有面無體者，太陽之為物大矣，知其必有體也。凡自然生者，初生者，無物不圓。太陽之生，亦本自然，曾無雕琢，初生則然，會無遷變。又諸體中，圓為最尊，以太陽較天下有形之物，亦是最尊，知其必為圓體」也。

　　《論太陽之大○》欲知物大，先知其徑。徑有二，一為視徑。視徑者，人目所視也。舊云太陽之徑一度，近來測驗，實止半度。

　　太陽之大視徑半度圖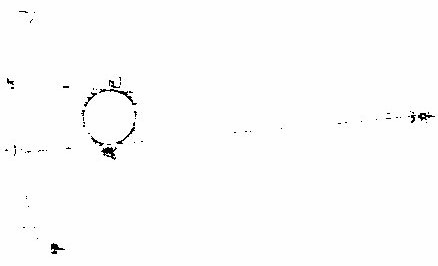

　　

　　太陽之大視徑半度圖說

　　如上圖甲乙乙丁丁戊為宗動天內規面之三度，入從辛，視太陽之己庚，徑于天度僅得丙丁，不滿乙丁之一度，約如乙丙者七百二十，則滿黃道周，故知視徑為半度也。

　　一為本徑。欲知本徑，先論其去地之遠。太陽去地有時近，有時遠，折取中數，則以《地全徑》為度。

　　里數太多難計，故以「地徑」之里數為其尺度也。地之周約九萬里，其全徑約三萬里，

　　二十四，其地徑自乘之，得五百七十六，是太陽去地之中數也。

　　其《比例》云：「地之徑與太陽去地之半徑若一與五百七十六也。」

　　既知其視徑，又得其去地之遠。因以《割圓術》求其本徑，得太陽之容，大于地之容一百餘倍也。

　　《論太陽之光○》：日為大光，六合之內，無微不照，有不透明之物，隔之則生影。地在天中，體小于日，故影漸遠漸殺，以至于盡。其影之長，不至太陽之衝。

　　論太陽之光圖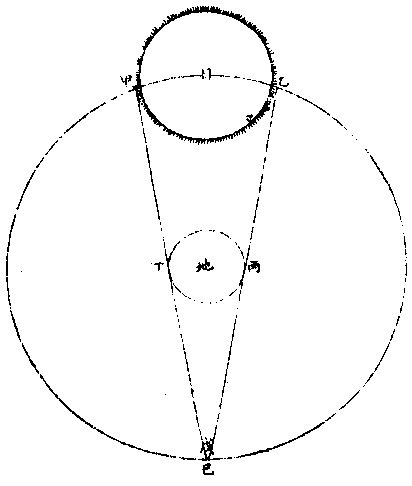

　　

　　論太陽之光圖說

　　如右圖，甲乙為日，丙丁為地，其景至戊而止，不至己。

　　太陽面上有黑子，或一或二，或三四而止，或大或小，恆於太陽東西徑上行，其道止一線，行十四日而盡。

　　前者盡則後者繼之，其大者能減太陽之光。先時或疑為金水二星，考其躔度則又不合。近有《望遠鏡》，乃知其體不與日體為一，又不若雲霞之去日極遠，特在其面而不審為何物。

　　《從運動論》

　　太陽之動有二：其一與「黃赤道比論，其一與《地平比論》。」

　　《與黃赤道比論○》，如從冬至一點起算，行天一日一周，明日不在冬至，即此一圈作螺旋一周。次日復然，迄夏至點行一百八十餘周，而通作一螺旋線也。第冬至線與次日一周線相離甚近，以次漸遠，迄春分而甚遠，過此漸近；迄夏至而甚近，過此又漸遠，如是循環無窮耳。

　　又冬至初日之線，其螺圈甚小，次日漸大，至春分甚大；過此漸小，迄夏至而甚小。如是小大循環者，何也？為緯圈中冬、夏至皆小圈，赤道為大圈故也。從冬至迄夏至，此為成歲之半矣。若從夏至迄冬至，亦作螺旋行，每日一周百八十餘日，通作一螺旋線。但此線非復前線，而別作一線，每日與前線作一交耳。此為成歲之全也

　　太陽一歲運動作二十四螺旋圈圖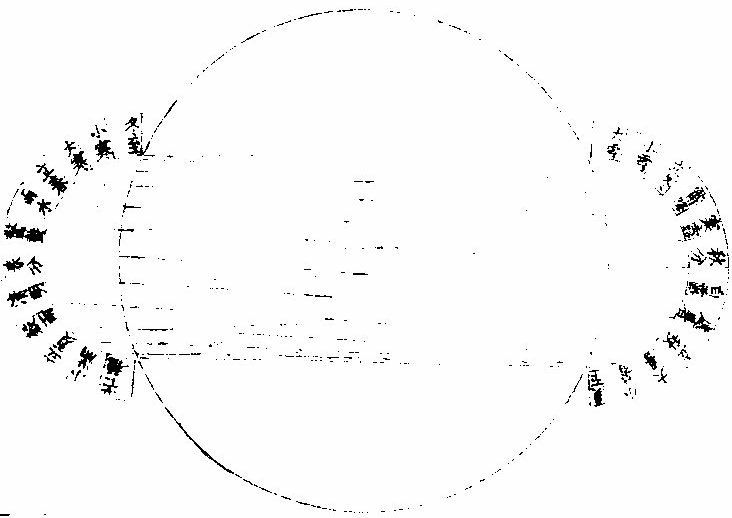

　　

　　太陽一歲運動，作《二十四螺旋圈圖》說。

　　如圖作螺旋圈，不能為三百六十作二十四，以明其意。已上所說螺旋線，是太陽之體理，實作如是運動，無可疑者。但螺旋則無法之線也，以此測候，亦復無法可立，故天官家別用他術如下文。

　　測候之術○，如用「春分起算初日，從初點循赤道行迄一周，是為一日。明日即不在赤道，而在其第二圈，又不直距于初點，而東西相去為黃道之一長度，其南北距度即不及一度也。此一周即為赤道之一距等圈矣。太陽恆在黃道下行，故無黃道之廣度。」至第三日，復作第三距等圈，與次日同。凡九十日行黃道九十度，即于赤道旁作九十距等圈。其第九十則夏至圈。夏至圈去春分圈止二十三度半，故太陽之行亦如是而止。此九十距等線以當全螺線之半也。用此術則從夏至迄秋分亦有九十距等線，其線即春夏距等之原線矣。

　　至秋分即復行赤道，一日無距度，距圈與前春分日所行同線相對，其兩對處則有極分交圈以為之限也。自春迄秋，二分之間，行一百八十度，黃道長度與赤道之距度其數皆等。從秋分而後，每日作一距等圈。其第九十則冬至圈也。凡諸距度圈皆交于黃道，獨二至之兩圈切于黃道，為其行至是盡矣。其兩盡處，則極至交圈為之限也。秋分迄冬至，亦二十三度半，與其迄夏至等，故其間距等圈與其迄夏至之距等圈亦等。從冬至以後，亦依前所行距等原線，以迄春分而歲成矣。

　　「太陽之行恆在黃道下，無廣度，亦恆在兩至之內。故兩至之內，皆為太陽所行之道，而太陽每日行一度弱，故兩至間之距等圈，凡一百八十二有奇，每一圈歲兩經焉。」如此術即分太陽所行為二路。其一，分計每日所行，各行于赤道，似圈皆在兩赤道極之間；其二，總計每歲所行皆行于黃道，在兩黃道極之間。其一日一周于黃道為一長度；于赤道上不及一上度，此一上度弱者，名為「黃道一日之升度。」黃道之升度，每宮與赤道不等，故每日黃道之升度一一不等。

　　《螺旋合術與黃赤分術比論》

　　論《合術》則自東而西，每日不及一度，故云「日遲。」論分術則自西而東，每日循黃道行一度，故云「日疾。」其實一也。但螺旋于理甚合，而無法可推；分術則分數易明，其間即有參差，不能及一微一纖，非儀象可測；故曆家專用分術。〈加減法也〉以便推步。

　　《與地平比論》

　　太陽至地平上，為出，為明；從東而西，沒於地平下，為入，為晦。

　　論正球春分日，太陽出于東方，行赤道，赤道即東西圈，漸升至頂極，即至南北圈，為極高之弧。此地平以上之半晝分也。亦謂之東半晝弧。午正後漸降至地平，謂之西半晝弧。東西合則為全弧，行盡全弧為一晝。

　　其一日之中，地平上，凡有表即得影，日出則為無窮之西影漸短，至頂僅得一點。

　　或云：「是為無影，安得一點？」不知無表即無影，若令表離于地平，即有與表等大之影。

　　午正後，影漸長，至地平，復為無窮之東影。日既入地平下則有朦朧分。〈一名昏度一名黃昏〉行地平之低度十八後，此為夜。

　　「低度」者，非黃道、赤道之度，乃地平之緯度也。在下，故名「低度，在上名高度。」

　　太陽與地平比論第一圖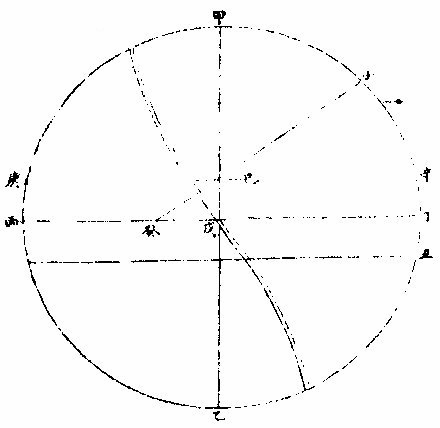

　　

　　《太陽與地平比論》第一圖說：

　　如上圖，甲乙為赤道即東西圈，丙甲丁為南北圈，甲高九十度，滿一象限，己戊為表，日出辛表端影在庚，至壬影在癸，至庚則在辛也。至甲止一點，丙丁即地平低度，十八至于丑而止。

　　日至于南北圈下，為半夜迨，近地平下十八低度，復為朦朧分。

　　一名《晨度》，一名昧旦，一名黎明，一名《昧爽》。

　　凡黎明將盡，日將出，地平上有雲，則為朝霞。黃昏之始，日初入地平上有雲，則為晚霞。所以赤色者，為日光返照，如火出煙。本是黑色，與火並見，即黑見煙，不見火，即為紅煙矣。

　　問：「日出入則大，日中則小，何故？」曰：「地居天中，日周其外，因於太陽，如受燔炙，恆出熱氣，是名清蒙之氣。此氣之厚，去地不能甚遠。日出入時，人目衡視積氣甚多，如物在水中，其體大於本體，故出入時，日形似大，非果大也。至日中時，以垂線照地，人直視之，積氣甚少，日不受蒙，則似小矣。若出入時，或深紫，或微紅，或」似長圓，亦皆是氣之厚薄疏密所為也。

　　其春分，夫日太陽離赤道，即不出於東西圈之初度，而在其稍北之闊度。

　　即地平之經度，不言「廣」者，以別於黃道緯度也。

　　其相去也與其日之距度等。

　　「為正球」，則赤道與地平為直角故也；欹球，則否。

　　太陽既稍北，則其表影亦稍南，其晝分與初日等。其南北圈下之極高弧，則稍減於九十度。又次日則闊度愈大，極高弧愈小。以迄夏至，其闊為二十三度有奇，其高弧為六十三度有奇。從赤道南迄冬至，亦如之。其方之晝與夜恆等。何者？赤道與地平為直角，即一切經緯圈，其隱見恆相半故。

　　太陽與地平比論第二圖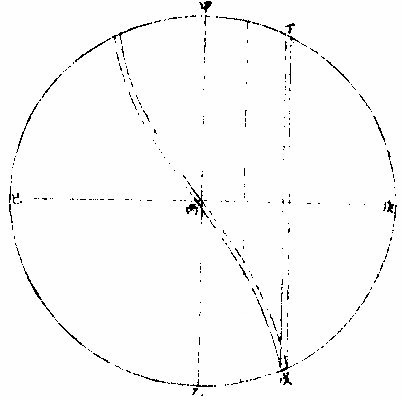

　　

　　《太陽與地平比論》第二圖說

　　如上圖，甲乙為赤道，即東西圈，春分日，日從此道行，次日以後，漸向丁戊行。甲至丁，乙至戊各二十三度有奇。庚至丁，其高弧六十六度有奇。

　　論欹球一歲中獨春秋分兩日得晝夜平，何者是其日太陽在赤道下，赤道與地平皆大圈，交而相分，即所分之圈分相等。若赤道距等圈大小不等，以地平分之，其圈分上下皆不等。

　　太陽與地平比論第三圖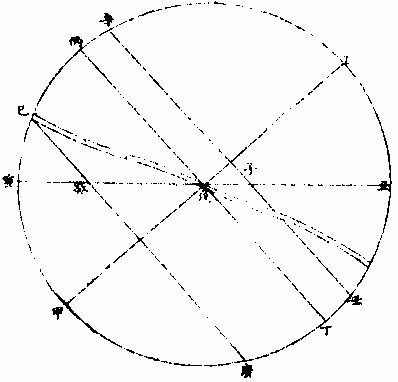

　　

　　《太陽與地平比論》第三圖說

　　如上圖，甲乙為南北極，丙丁為赤道，丑寅為地平。春秋分兩日，日在戊，為黃赤道之交，則地平上下圈分等。過春分日漸北，如至辛壬距等圈，則丑寅地平分晝夜于子；過秋分日漸南，如至己庚距等圈，則地平分晝夜于癸，上下皆不等。又一歲之中，凡兩晝之距、兩至等，則其晝分之長短亦等。凡兩晝之距、兩分等，即一在赤道南，一在赤道北，其距度等，而此日之晝與彼日之夜等。

　　凡球愈欹極，愈高即高至。〈不日冬夏至而日高至通南北言之〉之，日愈長。凡正球之南北闊度等，欹球則否。

　　凡正球之二至日中時，其高下恆相等；欹球，則否。日中時，其二至，一甚高、一甚低。

　　論平球，則以半年為一晝，以半年為一夜。何者？北極與頂極合，即赤道與地平亦合。故九十距等圈，從赤道迄一至，皆在地平上，其在下亦如之也。其表恆作無窮，及最長影不作短影。每日為一周，亦作十二時或二十四，但百八十周恆在晝耳

　　《論朦朧》〈早為晨分暮為昏分或井曰晨昏或省曰朦曰朦影朦度〉

　　太陽在二點，二點之距一至等，其朦亦等，何者？去至等則同在一距等圈上故。

　　若二點之距一分等，其朦不等，孰大孰小？近于上極者則大，遠則小。

　　北極出地處，則北六宮之朦大于南六宮，南極出地處反是。

　　北極出地處，太陽在北六宮愈近夏至，朦愈大，迄夏至極大，過夏至漸小。南方近冬至愈大，迄冬至則極大，過冬至漸小。北極出地處迄冬至不極小，極小者，在赤道冬至之間。南方迄夏至不極小，極小者，在赤道夏至之間。

　　太陽在北六宮，愈北朦愈大。

　　平球之處，其太陽入地低度不過二十三，去朦度之十八未遠也。故其晨昏最長。一年之中，明多於晦，幾乎不夜。

　　正球上兩點，在赤道南北，其距赤道等，其朦亦等；其距赤道不等，其朦亦不等。愈大愈遠，赤道者愈大。故二至之朦甚大，二分之朦甚小。

　　問：「欹球北極出地處之朦，夏至極大，而冬至不極小，極小者在赤道冬至之間，然則安在？」曰：「此在秋分之後，特隨地不同，皆在分後至前，不在其日也。如北極出地四十度，春分則六刻三十三分，夏至八刻六十分，秋分六刻三十三分，冬至則七刻，最小者六刻二十六分有奇，在寒露之中，候五日也。」

　　《湯若望新法曆引》

　　《日軌》

　　「太陽之行黃道也。」論其積歲平分之數，新法以天度計為五十九分八秒有奇，所謂平行度分是也。然平行齊而實行則周，非齊矣，冬盈而夏縮矣。所以然者，蓋緣黃道圈與日輪天不同心，而黃道之心即地球心，是日輪天與地球不同心也。心既不同，則日行距地近遠不等，距近即行疾，疾則所行之度，過于平行「而為盈。每冬月一日，計行一度一分有奇，以較平行，盈二分矣。距遠即行遲，遲則所行之度，不及平行而為縮。每夏月一日，計行五十七分有奇，以較平行，則縮二分矣。盈縮相差若此，豈可謂之齊乎？終歲之間，但逢最高限、最卑限二日，平實二行，度數惟一。」此外兩行之較，日日不等。新法因其或過或不及也，故有加分減分，謂之加減差。葢以有恆率之平行為根，而以加減差定之，然後差而不差，非齊而齊矣。至論太陽之入某宮次以分節氣也，亦有平實二算。葢算平行十五日二十一刻有奇，為一節氣，乃一歲二十四平分之一耳。若用躔度之日以算，則冬夏不齊。冬一節氣為十四日八十四刻有奇。夏一節氣。為十五日七十二刻有奇。總由夏遲冬疾。故其差如此。皆非《舊曆》之所解也。

　　太陽天距地極遠之點謂之「最高」，極近之點謂之「最高衝。」〈亦名最卑〉此二點者，乃盈縮二行之界。古法於冬夏二至，謂其恆在一點，其實非也。按古今諸測，皆各不齊。古測最高在夏至前數度，今則在後六度矣。以此推知，一年之內，太陽自行四十五秒也。

　　《測食》

　　《日食在朔月體揜之》

　　問：「月在日前能揜日光，金水二星亦在日前，又皆實體。且水星雖小，而金星則大于月，何獨以食屬月乎？」曰：「二星于人甚遠，不能掩日百分之一二，而日光漸盛，即虧百分之一二，人亦不覺。且二星去日甚近，去地甚遠，所出銳角之影亦甚短，決不能及地面。若夫月體雖不及太白之大，然去地近，去日遠，一指足蔽」泰山，又何疑乎？由此言之，求一「實體」之能全掩日，又從西而東，過之甚疾，唯月為能。蓋月之右旋，比諸天更速，且必至合朔方食。則日食於月，決然之理也。

　　《曆象圖說》

　　日蝕三差圖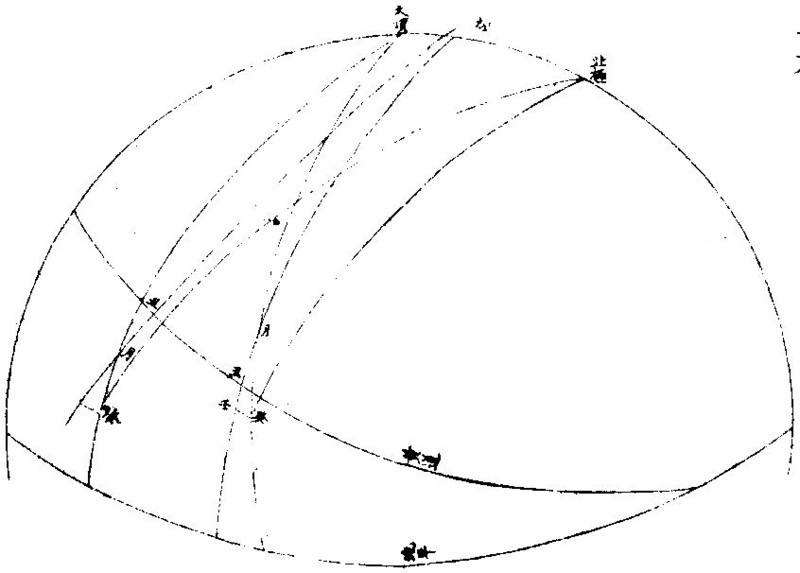

　　

　　日蝕三差圖說

　　一南北差能變緯度，而使蝕分有多少；一東西差能變經度，而使加時有早晚。皆以高卑差為本，即地半徑視差也。三差共成一勾股形，高卑差，其弦南北差，其股東西差，其勾云如地心指，實高于月，而地而視高在癸，則月癸即高卑差。此差以天頂為宗，月距黃道丑為實，緯度因高卑差而視緯變為丑壬，則月壬即南北差。此差以黃道極為宗，從黃道極定實經度于丑而至壬，因高卑差而視經變而至癸，則壬癸為東西差，即黃道上弧度也。推三差，以差角為本，如月下至地平為高度，而以月距天頂〈高度之餘〉與月距黃道極為兩腰，而天頂距黃道極為對角之底。所得之差角與壬月癸角為交角，其度等。以差角之正線取東西差，以差角之餘線取南北差，而差角之餘角名高度交分，則以月距天頂與月距中限為兩腰，而中限高度為對角之底，所得之角即差角之餘，故取南北東西差與差角相反。推差角又以極至交圈交於子午圈之角為本，如月距天頂又距黃道極，則先有北極之交角。以北極距天頂與北極距黃道極為兩腰，而黃道極距天頂為對角之底，即有午位黃道之交角。以月午位與午位黃道距天頂為兩腰，而月距天頂為對角之底。得此極交分而後可求差角，得差角而後可求三差。用加減交食之分秒時刻，乃與所推所測之地人目所見相合，故謂之「視會。」此古來曆術未發之奧義也。

　　《曆象圖說舊本》

　　九服見蝕圖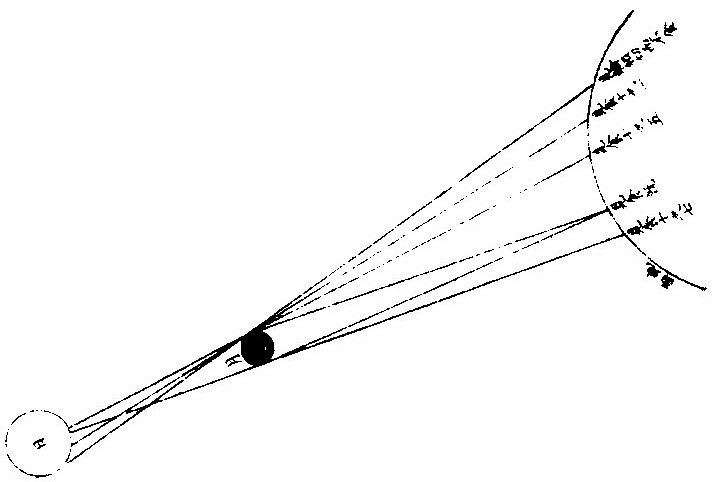

　　

　　九服見蝕圖說

　　月魄掩日，而日為之蝕。故正當月魄之下，即見蝕既。

　　地平，經緯漸差，所見蝕分，多寡遂異。蓋由日高月下地偏，則所見非經緯相合之一線，漸視兩體空際，而所掩漸覺其少。故日蝕之分，隨方不同，非如月蝕，普天同視也○。《黃鐘曆議》云：「舊云月行內道，在黃道之北，蝕多有驗。月行外道，在黃道之南，雖遇正交，無由掩映，蝕多不驗。」又云：「天之交限雖係內道，若在人之交限之外，類同外道，日亦不食。」此說似而未盡。假如夏至前後，日食於寅卯酉戌之間，人向東北西北而視之，則外道食分反多於內道矣。按內外道即陰陽曆也。月行陰曆為內道，則有北緯，行陽曆為外道，則有南緯。古法日食求差，以赤道午線為中，則日食距中之度，或大於象限，故《授時曆》東西南北差有反減法，《黃鐘曆議》之說，葢出於此。今法以黃平限為中，可無此疑。何則？日食三差，並以高下差為根。〈詳見後條〉黃平限恆居天頂之南，而人居其北，北高南下，故能以北緯變南緯，無南緯變北之理，冬夏一也。惟地近交廣極出地在二十三度以下，黃平限有時在天頂之北，則其時南緯可以變北耳。〈南緯變北則外道食分反多恆此時為然〉

　　日食三差圖二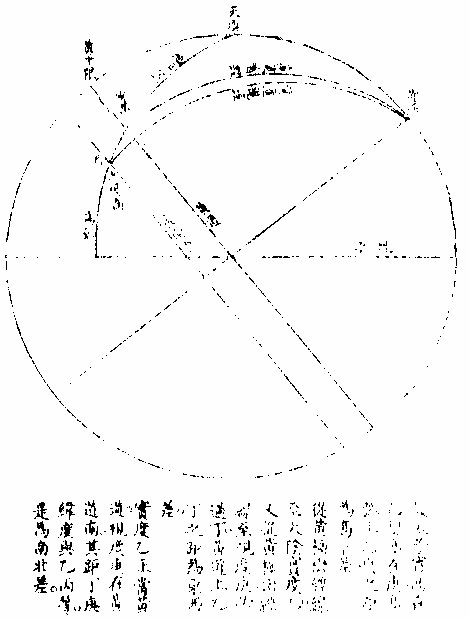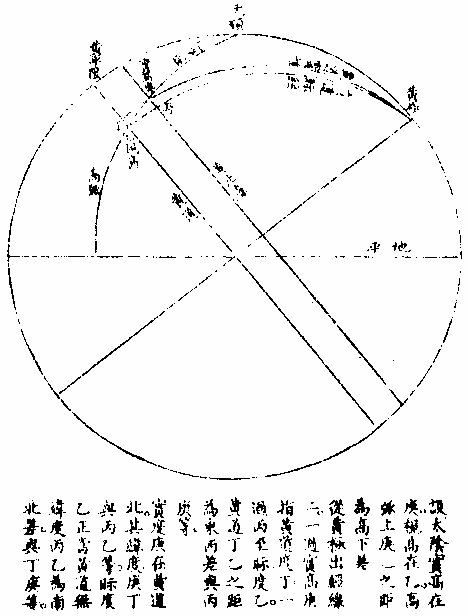

　　

　　日食三差圖三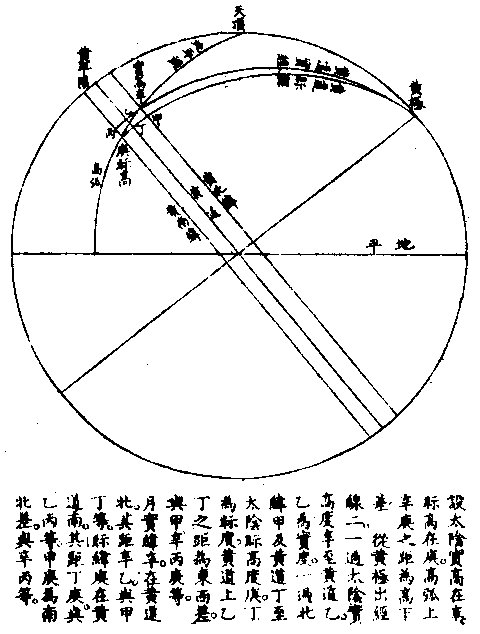

　　

　　日食三差圖說

　　推步日蝕，為曆法至要而至難。即立法精微，布算巧密，而所推與所測往往不符。蓋有東西差能變經度，而交蝕之時刻遂有早晚；南北差能變緯度，而交蝕之分秒遂有淺深。此兩差以「高卑差為本，凡自地心指其實度之高，及自地面觀之，必在實度之下。其差降高為卑，而象句股之有弦，然後東西差與黃道平」行而為之句。從黃極出經線，遇句弦，以限南北差而為之股。極南則弦與股合而無東西差。極東、極西則弦與句合而無南北差也○。地心、地面之說，古未有也。《新法》謂地體正圓，而正居大圓之中，則地心即天心也。凡曆家測驗，自地平圈起，初度升至九十度而為天頂者，皆正與地心相應，而人所居則在地面，穹窿而踞地心之上，徒以體圓勢順，目所環觀，得睹大輿之半，因以謂之「地平。」若用以直天度，則惟恆星天距地絕遠，視地甚小，可無推心面之差。若日天則居七政之中，月天則距地最近，去日猶遠。是以心面之間，高下生焉。高下之間，南北東西異焉。蓋有推得地心，日食而地面不食者；亦有地心未應食，而地面旁視反見食者。於是東西之差，則有時刻之早晚；南北之差，則有分數之淺深。人但知里差之法為加時分秒之由，不知同一分域而地心地面原有兩差，為差之根也○。地心之所見惟一，而地面之所見，隨處不同。故日食三差，生於地圓；而九服見蝕，生於三差也。

　　〈假令人居地心則東西南北之差無從可立而萬形一視矣故三差皆地面所生而遂有九服之各異〉北齊張子信謂日食有入氣差。至唐長慶中，《宣明曆》遂有刻氣時、三差之怯，歷代因之。郭守敬正其名曰「東西差、南北差。」今則以地圓之理著其所以然者。

梦远书城(guxuo.com)