古今圖書集成·乾象典第二十九卷

第二十九卷

　　日月部彙考一

　　《易經》

　　《離卦》

　　日月麗乎天，

　　《豐卦》

　　日中則昃，月盈則食。

　　《繫辭上傳》

　　縣象著明，莫大乎日月。

　　〈大全〉進齋徐氏曰：「天文煥爛，皆懸象著明也，而莫大乎日月。」

　　《繫辭下傳》

　　「日月之道」，貞明者也。

　　〈大全〉程子曰：日月常明而不息，故曰「貞明。」

　　又

　　「日往則月來」，月往則日來。日月相推而明生焉。

　　〈大全〉臨川吳氏曰：「因日之往而有月之來，因月之往而有日之來，二曜相推以相繼，則明生而不匱。」

　　《書經》

　　《周書洪範》

　　日月之行，則有冬有夏。

　　〈疏〉日月之行，四時皆有常法，變冬夏為南北之極，故舉以言之。日月之行，冬夏各有常度，喻人君為政，大小各有常法。張衡、蔡邕、王蕃等說，渾天者皆云：「周天三百六十五度四分度之一，天體圓如彈丸，北高南下。北極出地上三十六度，南極入地下三十六度，北極去南極直徑一百二十二度弱，其依天體隆曲。南極」去北極一百八十二度，彊正當天之中央，南北二極中等之處，謂之「赤道」，去南北極各九十一度。春分日行赤道，從此漸北。夏至赤道之北二十四度，去北極六十七度，去南極一百一十五度。日行黑道，從夏至以後日漸南，至秋分還行赤道，與春分同。冬至行赤道之南二十四度，去南極六十七度，去北極一百一十五度，其日之行處謂之「黃道。」又有月行之道，與日道相近，交路而過，半在日道之裏，半在日道之表。其當交則兩道相合，交去極遠處，兩道相去六度。此其日月行道之大略也。

　　《詩經》

　　《邶風日月章》

　　日居月諸，出自東方。

　　〈傳〉「日始月盛」，皆出東方。

　　《周禮》

　　《春官》

　　《馮相氏》「冬夏致日，春秋致月。」

　　〈訂義〉王昭禹曰：「日為陽而實，故致於長短極之時；月為陰而闕，故致於長短不極之時。」鄭康成曰：「冬至日在牽牛，景丈三尺；夏至日在東井，景尺五寸。此長短之極，極則氣至。冬無愆陽，夏無伏陰。春分日在婁，秋分日在角，而月弦於牽牛、東井，亦以其景知氣至否。」陸佃曰：「黃道北至東井，南至牽牛，東至角，西至婁；夏至日在東井而北，近極則晷短，而表景尺五寸。冬至日在牽牛而南，遠極則晷長，而表景丈三尺。春分日在婁，秋分日在角，而中於

　　「極星，則晷中而表景七尺三寸。」夫日陽也，陽用事則日進而北，晝進而長，陽升故為溫為暑；陰用事則日退而南，晝退而短，陰勝則為涼為寒。若日失節於南，則晷過而長為常；寒失節於北，則晷退而短為常。燠！此四時致日之法也。月之九行在東西南北，有青白赤黑之道各二，而出於黃道之旁。立春春分，月循行「青道，而春分上弦在東井。立冬、冬至，北旋黑道；立夏、夏至，南從赤道。」古之致月，不在立而常在二分，不在二分之朢而常在弦者，以月入八日與不盡八日，得陰陽之正平故也。然日之與月，陰陽尊卑之辨，若君臣然。觀「君居中而逸，臣旁行而勞，臣近君則威損，遠君則勢盛，威損與君異，勢盛與君同。」月遠日則光盛，近日則光缺，未朢則出西，既朢則出東，則日有中道，月有九行之說，蓋足信也。

　　以辨四時之敘。

　　〈訂羲〉鄭鍔曰：「辨』字本亦作，辯說者，謂見景之至否，可以辯說其晷刻，以正閏餘，使四時之敘無有差忒。

　　黃氏曰：「夏至日景極長，冬至日景極短，春秋分。」

　　平日景平則日亦平致，言長短與平，各至其數，四時之氣定矣。於是而置閏，所謂「以閏月定四時成歲」也。

　　《禮記》

　　《月令》

　　季冬之月，「日窮於次，月窮於紀。」

　　〈註〉次，舍也。紀，會也。〈疏〉「日窮於次」者，謂去年季冬，日次於元枵，從此以來，每引移次他辰，至此月窮盡，還次元枵。「月窮於紀」者，去年冬季，月與日相會於元枵，自此以來，月與日相會在於他辰，至此月窮盡，還復會於元枵。

　　《易緯》

　　《稽覽圖》

　　日：春行東方青道曰「東陸。」

　　夏，日月行東南赤道，曰「南陸。」

　　「《天》有十二分」，以日月之所躔也；

　　《管子》

　　《四時》

　　日掌陽，月掌陰。

　　《漢書》

　　《天文志》

　　「日有中道，月有九行。」中道者，黃道，一曰光道。光道北至東井，去北極近；南至牽牛，去北極遠；東至角，西至婁，去極中。夏至至於東井北，近極，故晷短，立八尺之表，而晷景長尺五寸八分；冬至至於牽牛，遠極，故晷長，立八尺之表，而晷景長丈三尺一寸四分。春秋分日至婁角，去極中，而晷中立八尺之表，而晷景長七尺三寸六分，此日去極遠近之差，晷景長短之制也。

　　月有九行者，黑道二，出黃道北；赤道二，出黃道南；白道二，出黃道西；青道二，出黃道東。立春、春分，月東從青道；立秋、秋分，西從白道；立冬、冬至，北從黑道；立夏、夏至，南從赤道。然用之一決房中道。

　　〈注〉宋祁曰：「朱子文云：『房』字當作『於』字。蓋言月之行其道雖多，然皆決於日之中道也。」

　　《淮南子》

　　《天文訓》

　　積陽之熱氣生火，火氣之精者為日。積陰之寒氣為水，水氣之精者為月。

　　日者，陽之主也。「是故春夏則群獸除，日至而麋鹿解。

　　月者，陰之宗也。是以月虛而魚腦減，月死而《蠃蛖膲》。

　　日月者，天之使也。」

　　日為德，月為刑，月歸而萬物死，日至而萬物生。

　　《劉熙釋名》

　　《釋天》

　　日，實也。光明盛實也。

　　月缺也，滿則缺也。

　　光，晃也。晃晃然也。亦言廣也。所照廣遠也。

　　景。境也。明所照處有境限也。

　　晷，規也，如規畫也。

　　曜，耀也。光明照耀也。

　　《揚雄方言》

　　《日月運行》

　　《躔歷》，行也。日運為躔，月運為逡。

　　《白虎通》

　　《日月》

　　「天左旋，日月五星右行何？日月五星比天為陰，故右行。右行者，猶臣對君也。」《含文嘉》曰：「計日月，右行也。刑德放日月東行，而日行遲，月行疾何？君舒臣勞也。日日行一度，月日行十三度十九分度之七。」《感精符》曰：「三綱之義，日為君，月為臣也。日月所以懸晝夜者何？助天行化，照明下地。故《易》曰：『懸象著明，莫大乎日月』。」日之為言實也，常滿有節；月之為言闕也，有滿有闕也。所以有闕何？歸功於日也。八日成光，二八十六日轉而歸功，晦至朔旦，受符復行。故《援神契》曰：「月三日成魄也。」所以名之為星何？星者，精也，據日節言也。一日一行，適行一度，一日夜為一日，剩復分天為三十六度，周天三百六十五度四分度之一。日月徑千里也。所以必有晝夜何？備陰陽也。日照晝，月照夜，日所以有長短何？陰陽更相用事也。故夏節晝長，冬節夜長。夏日宿在東井，出寅入戌；冬日宿在牽牛，出辰入申。月大小何？天道左旋，日月東行，日日行一度，月日行十三度，月及日為一月，至二十九日未及七度，即三十日者過行七度。日不可分，故月乍大小，明有陰陽。故《春秋》曰：「九月庚戌朔，日有食之」，「十月庚辰朔，日有食之。」此三十日也。又曰：「七月甲子朔，日有食之」，「八月癸巳朔，日有食之。」此二十九日也。月有閏餘。《何周天》三百六十五度四分度之一歲十二月，日過十二度，故三年一閏，五年再閏，明陰不足陽有餘也。故讖曰：「閏者陽之餘。」

　　《魏張揖廣雅》

　　《日月》

　　《朱明曜靈》，東君日也。夜光謂之月，日御謂之羲和，月御謂之「朢舒。」

　　《吳徐整長曆》

　　《日月徑》

　　「眾陽之精」，上合為日，日徑千里，周圍三千里，下於天七千里。

　　《月徑》千里，周圍三千里，下於天七千里。

　　《晉書》

　　《天文志》

　　「天旁轉如推磨而左行」，日月右行，隨天左轉，故「日月實東行，而天牽之以西沒。」

　　《五代史》

　　《司天考》

　　日食起虧自西，月食起虧自東。其食分少者，月行陽道，則日食偏南，月食偏北；陰道則日食偏北，月食偏南：此常數也。立春後、立夏前，食分多，則日食偏南，月食偏北；立秋後、立冬前，食分多，則日食偏北，月食偏南：此黃道斜正也。陽道交前，陰道交後，食分多，則日食偏南，月食偏北。陽道交後，陰道交前，食分多，則日食偏北，月食偏南，此九道斜正也。

　　《張子正蒙》

　　《參兩篇》

　　日質本陰，月質本陽，故於朔朢之際，精魄反交，則光為之食矣。

　　《虧盈法》：月於人為近，日遠在外，故月受日光，常在於外。人視其終初如鉤之曲，及其中天也，如半璧然。此虧盈之驗也。

　　月所位者陽，故受日之光，不受日之精，相朢中弦則光為之食，精之不可以二也。

　　《明羅雅谷交食曆指》

　　《界說》

　　凡物體能隔他物之象，使不至目，則為「暗體。」若以體之一面受光，而光復透射出於彼面，則為「徹體。」〈如玻璃水精是也〉○目所司存，惟光惟色，而色又隨光發見，故解「徹體」，必以通光，解「暗體」，必以其能隔他象。如月掩日而日全食，晝為之晦，恆星皆見。爾時太陽在外，體質明顯，又堅密無比，光力甚厚，乃為月體所隔，不能映見微光可證。月乃全非徹體，而全為暗體○。徹體有二，通明之極，全無隔礙者為甚徹；雖則透光，而微雜昏蒙者為「次徹。」

　　光在本體為原光，其出而顯他物之象為照光○。日有原光，地與月皆借之為光者，照光也。謂顯他物之象者，因他物之勢隨施隨受，有原先後，無時先後也。

　　非如寒熱燥濕之類，漸及於物，力盡而止。

　　《原光》以直徑發照為最光，因而旁及者為次光○。日光正照以直線至於物體，則為最光。有物隔之，旁周映射，則生次光。如雲之上，日體所照，最光也。雲之下，不復見日，而猶有光，是次光也。

　　滿光者，原光之全體所發。少光者，原光之半體所發○。日未全出地，平上所生光為少光。全升在上，則生滿光。日食時未全食，則存少光。既以復圓，即得滿光。

　　景之四周有最光遶之，即景為次光○。以景為明者，誤也；以影為暗者，亦誤也。稱景為明暗之中，庶幾近之，蓋全無光乃為暗。今至夜子初，人在地景至深之中，去最光極遠，而近目之物尚能別識，即見景中猶存微光，不失為「次光」也。

　　最光所不及為「初景」，次光所不及，則為「次景○。」景與光并行，光漸微，景漸厚，故「次景」與「最光」相反。若初景，即次光也。

　　最光全不及之處，則為「滿景。」若受正照之微光，即為「缺景○。」景與光正相反，無景之極則為「滿光」，無光之極則為「滿景

　　光景圖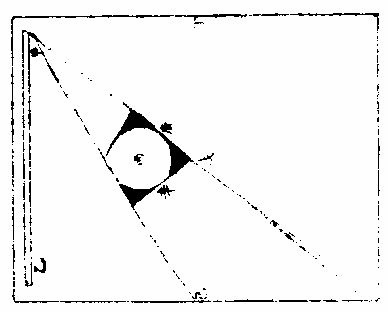

　　

　　光景圖說

　　假如甲乙為施光之物，丙為暗球，從甲出正照之光過丙球左右，其切丙之界者，得甲戊及甲己，從乙出光，又得乙戊及乙丁。其庚戊辛為最光，全不及之處則滿景也。若庚戊辛戊以外，則甲乙光體之多分，漸照之至乙丁甲己乃全光之界，即自戊至丁至己，丙球之景漸薄以趨于盡矣。

　　《太陽光照月及地》

　　日月地三，球體大小不等。地為靜體，日月則有諸種，行度則有高庳內外。其去地去人遠近不等。法當以大小之比例及其相遠相近之比例，推其施光受光之體勢，乃得景之體勢，因而得交食之體勢。蓋交食者生于景，景生于光，不尋其本而求其末，無法可得。

　　其說五章。

　　明暗兩體相等圖

　　

　　《明暗兩體相等圖說》。

　　一曰：有兩球於此，一為暗體，一為明體，而小大等，即明者以半面施光，暗者以半面受光○。如圖甲為明球，乙為暗球，小大等，即其徑丙丁及戊己各與甲乙線為直角，而丙丁與戊己等，即甲丙甲丁，乙戊乙己與甲庚乙辛，皆以半徑相等，而丙庚丁半球，與戊辛己半球亦相等。今於明球之旁，從丙從丁出兩切線，至暗球之旁戊己，戊己與丙丁為平行線，即丙戊與丁己亦平行線也。又因丙戊乙及丁己乙俱為直角，即戊丙甲及己丁甲亦俱直角，即丙戊丁己線不能割兩球，而止切兩周於丙於戊、於丁於己，其所抱為丙庚丁、為戊辛己，是甲乙兩球之各半也。若日月地三球相等，而月與地皆以半面受太陽之光，如上所說，則定朔日食，半地面宜皆見之，安得復有南北不等食分？朢日，太陰全食時，纔食既即生光，安得復有食甚時刻及既內分？今皆不然，可見三球無相等之球。

　　明體大暗體小圖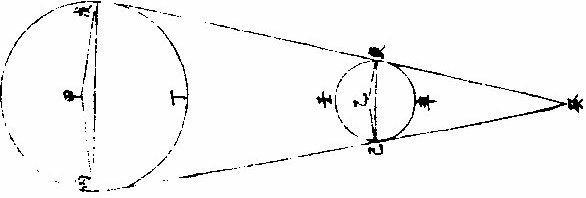

　　

　　「明體大、暗體小」《圖》說。

　　二曰明體大，暗體小，則施光以小半，受光以大半○。

　　如圖甲為明球，乙為暗球，作兩切線，為丙己，為戊庚，從四切點作橫線，為丙戊，為己庚。甲既大球，即己丙戊為銳角，丙己庚角為鈍角。如曰不然，或皆為直角，即庚戊丙戊庚己亦皆直角，兩切線必平行，而乙球與甲球等，必不然也。或己丙戊反為鈍角，而丙己庚反為銳角，即兩切線不能相交于癸，又不然也。今以兩切線相交于癸，明己丙戊為銳角，丙己庚為鈍角。

　　即于丙丁戊弧內作負圈角，必鈍角矣；于己壬庚內作負圈角，必銳角矣。故丙丁戊施光者不及半圈，己壬庚受光者又不止半圈也。因此推知太陽照地，及太陰必各照其大半，而暗體所隔之日光漸遠，又漸斂漸進以趨于一處，即景居暗球之背，不得不為角體之形矣。又因此推求朢日先後，人目所見，太陰受日之光不長不消者，久之而後生魄。此為何故？蓋亦因月體以大半受光，小半入于人目，光不輒轉，而魄未遽見，故未朢時已見全光，已朢後猶未失全光也

　　明體小暗體大圖

　　

　　「明體小、暗體大」《圖》說。

　　三曰：「明體小，暗體大，則施光以大半，受光以小半○」，如前《圖》反論之，可明太陰何以照地？而地何反隔日之光也？

　　大施小受圖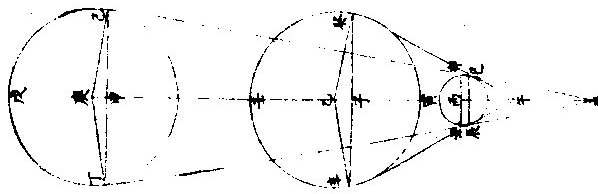

　　

　　大施小受圖說

　　四曰「大施」、「小受。」愈相近，則施者之小半愈小，受者之大半愈大○。如圖丙為小暗球，甲與乙皆大明球，作庚未直線，過三球心，以交於左右切線。其乙球之兩切線交于午，甲球之兩切線交于未，即庚未長于乙午，而庚丁未與乙辛午兩角，庚丁與乙辛兩線皆相等，則庚未線與庚丁線之比例，大于乙午與乙辛，而丁「庚未角大于辛乙午角也。又庚未線過三球之心，必截丁己辛癸兩線為兩平分，而庚甲丁乙子辛兩形內之甲與子皆為直角」，則其餘庚丁兩角并乙辛兩角并，皆等一直角，即兩并率等兩并率之甲庚丁角大于子乙辛角，各減之，所存庚丁甲角，必小于乙辛子角矣。次以庚丁甲及乙辛子不等「之兩角，各減庚丁未及乙辛午相等之兩直角，所存甲丁未角，更大于子辛午角，又《丁戊己弧》內作負圈角，必等于甲丁未角，《辛壬癸弧》內作負圈角，必等于子辛午角，《辛壬癸弧》之負圈角，既小于丁戊己弧之負圈角，則《辛壬癸弧》必大于丁戊己弧。夫辰寅巳與辛壬癸相似之弧也，丑寅卯與丁戊己」，亦相似之弧也。〈大小圈左右各有切線其切點過分圈之線其所分大小圈分各相似其大小兩弧亦相似〉即辰寅巳弧亦大於丑寅卯弧，可見明球在近比在遠者，尤能照小暗球之多分也○。因此推知日全食而視為大者，日體去月體遠故也。日全食而視為小者，日體去月體近故也。何以分遠近？日與月俱有自行圈，與地不同心，其行於自行圈之上下為最高最庳，則為距地之遠近，因生景之大小也。日既全食矣，又何以分大小？月掩日至，既有時晝晦，恆星皆見，蟲飛鳥棲，此為全食。而大月在日內，從中掩蔽，雖至食既，而其四周日光皆見，曆家謂之「金環」，此為全食而小矣。若然者，日與月與地，相去或遠或近之所繇生也。

　　小施大受圖

　　

　　小施大受圖說

　　五曰「小施。」大受。愈相遠，則施者之大半加小，受者之小半漸大○。如圖甲乙皆為小明球，丙為大暗球，乙去丙遠，于甲作各切線，過三球心之直線，皆如前。次從暗球心丙至各切點，作丙丁、丙己、丙庚、丙辛各半徑，得丙丁為丁壬之垂線，丙庚為庚癸之垂線，而丁與庚皆為直角，丙丁與丙庚兩線又等，則丙癸線與丙庚半徑之比例，大于丙壬與丙丁，而丙庚癸角又大于丙丁壬角也。依顯丙辛癸角亦大于丙己壬角以并前率為庚丙辛合角，亦大於丁丙己合角，而其弧庚戊辛必大於丁戊己。可見小明球照大暗球，愈遠愈照其多分也。今依本圖，設丙為地外切線。〈癸辛也〉以內為《地景》。〈日光過丙大球所出景〉甲、乙兩小球為月體。其兩小球之小大既等，則同以外切線為外光之界，或為內景之界。惟因月體循本輪行，時居上周如乙，則去地遠；時居下周如甲，則去地近。以是月食之分數有多有寡。月居影厚處，如甲左右，則食多；月居影薄處，如乙左右，則食寡。故曰：「月食有多寡」者，亦相距或遠或近之所由生也。

　　景之處所

　　凡光以直線照物，體其無光之處，則有景之處也。欲於交食時求影所在，理不異此。蓋月與地能出景者，不在其受光之面，或其左右必於受光反對之面。日光不照之地，在日食則為月景之處，在月食則為地景之處矣。《說》二章。

　　光景相反圖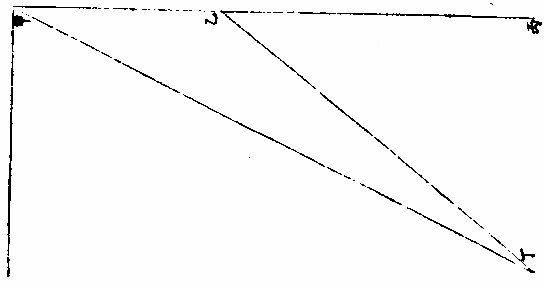

　　

　　光景相反圖說

　　一曰「景與光所居正相反○」，暗體得光于此面，射影于彼面，是景之中心，與原光之心、暗體之心參相對，如一直線，則暗體隔光于景，使原光之心恆居一線之末界，其正相反之彼界，其景之心在焉。如曰不然，設原光在甲，其照及乙，乙為暗體，隔光生景。據云：「景不射丙。」〈丙者與甲正相對之處〉為甲乙丙直線，而斜射丁則乙甲丁者角也，有角則有幾何，凡幾何，皆分之無窮，能出直線至于無數，而皆至乙丁邊。夫甲既為原光之體，其所照必以直線出之。〈試諸儀器足以為證〉即乙丁皆在受光之地，何自能為乙暗體之景乎？因此明景與光，正在相反之兩界。論暗體者，其受光之面，必向光所出之原界，其生景之面，必向景所射之彼界，亦正相反也。論日與月，獨至兩交之處而有食，亦依此理。

　　體動景移圖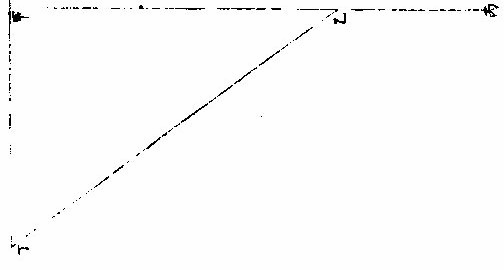

　　

　　體動景移圖說

　　「二曰，明暗兩體，任一運動，景隨之移○。試以暗體移動，其所借之光，隨處不一，即所生之景，亦隨處不一。

　　蓋景與光既如一直線，即暗體所居，定為景之末界。

　　如直線之首，首移而線尚不移，則是曲線，非直線也。

　　又試以明體移動，設甲為明體，乙為暗體，乙丙為影，則甲乙丙如一直線。如曰明體，甲移至丁，丁仍照乙，而乙尚射景至丙，則丁乙丙猶直線也，有是理乎？」問：太陽照室，僅通隙光，光照牆壁，奕奕顫動，太陽既自順行，牆隙仍無遷變，則此顫動為從何來？或者光與景未必定為直線，而能微作曲勢乎？曰：「西古博物者亞利斯多言空中嘗有浮埃，輕而不墜，微而不顯，莊周氏謂之野馬，或亦稱為白駒。幽室之」內，原光既微，次光反厚，即顯此物在于光中，紛入沓出，能亂光景之界，使目視景，絪縕浮動，而寔非景動，乃景之界線，為浮埃所亂，致使其然也。更以氣為證，今觀太陽出地，地面以上多生蒙氣，氣在日體與人目之間，即見日之光界，亦如顫動。非獨日也，日中晴朗，切視地面，光耀閃爍，如波浪然。熾炭在罏，炭之四周，火光煜煜，亦如顫動。凡若此者，一皆繇氣而生。在日在地在炭，固無顫動之理。是以景必繫於暗體，如輪必繫於樞軸，光上景即下，光東景即西，必相對也，無相就也。

　　故太陽照地，其光繞地一周，則景在其相衝之界，亦繞天一周。蓋日光從其本天直射至於地面，而景在地之彼面，亦直射至于月天，第日體常依黃道中線，則地景亦常依黃道中線，而月行常出入黃道中線之內外，是以月體與地景不得恆相遇合，大都不合時多，合時少，故日月不食時多，食時少，以此。

　　《景之作用》

　　月與地，若各以其景相酬報然。如月朢，則地景隔日光，令月不受照，有時失滿光，有時全失光也。至月朔，則月體隔日光，令地不受照，有處射滿影，有處留少光而已。《說三章》。

　　一曰「月食于地景○。」月食在朢，緣日月相對，其理明矣。獨謂闇虛為地景者，或致疑焉。今解之，月對日受光，藉非日月之間有不通光之實體為其映蔽，則何繇阻日光之直照？若天體及空中之火，空中之氣，皆通明透徹，不能作障，使月失光也。即金水二星亦是實體，有時居日月之間，然其景俱不及地，况能過地及月乎？則知能掩月者，惟有地體。一面受光，一面射景，而月體為借光之物，入此景中，無能不食，半進而半食矣，全進而全食矣。

　　「二曰日食者，月揜之○恆言。月在內去人近，日在外，去人遠，故定朔時，月體能揜日光是已。第金水二星亦皆時在日內，又皆不通光之實體，水星雖小，金星則大於月也，何獨月能食日乎？」曰：「二星雖有時在日內，則去人甚遠，遠則視徑見小，不能揜日百分之一二，而日光甚盛，所虧百之一二，非目力所及。且二星比」月去日更近，所出銳角之景更短，不能及地面也。

　　若月體之大，雖不及太白，而去地甚近，去日甚遠，一指足蔽泰山，又何疑乎？由此言之，求一實不通光之體，全揜日體者，惟月為能。又自西而東，不及三十日而周，其行度較于諸天最為疾速。故每朢定朔，皆同經度，皆能有食。其不食者，繇距度不及交耳。

　　三曰「因景之徑，生多變易○。月以距度廣狹為食分多寡：一因去交有遠有近，去黃道中線有正有偏，一因入地景有淺有深故也。」今論其全食者，而大小遲疾，猶多變易，曾非一定。蓋日在自行本天，月在小輪，相距遠近往往不等。日距月近，「較距遠時更照月體之多，分從月體出景更短，其景至地更小，則日雖全食」，月體見小，歷時亦速也。日與地亦然，以兩體相距之遠近為地景之大小。使月食時入于地景，在其近末之銳分，則闇虛之體見小食分少，歷時速。皆因三體之相距遠近以生大小遲疾。地景、月景皆無一定之徑，致令隨時變易如此○。若月景、地景二徑之小大又自不等。故日食盡於食既而月，則食既以後，尚有既內餘分。蓋地景大於月景，故兩食皆全，其虧復遲疾，無能不異矣。又月食天下皆同，日食則否。日食則此地速，彼地遲，此地見多，彼地見少；此地見偏南，彼地見偏北，無不異也。月食則凡居地面者，目所共見，其食分大小同，虧復遲疾同，經歷時刻同，唯所居不同子午線者，則見食之時刻先後不同耳。蓋月一入景，失去借光，更無處可見其光也。又概論天下日食，應多于月食，為二徑折半，其近交時，加以南北視差，易相逮及。故論一方，則日食應少于月食，為月食共見，日食因地故。

　　《日月食合論》

　　日食與月食不同勢，食日謂之障食，食月謂之藏食。

　　何謂「障食？」日為諸光之宗，月與星皆從受光焉。月之食日，非真食日也。《定朔》則地與月與日自下而上為一線相參直。月本暗體，今在日與地之間，以暗體之上半受光于日，以下半射景於地，如屏蔽然，特能下揜人目，而不能上侵日體，日之原光自若也。是故人見為食，而實非食也。何謂「藏食？」定朢則日月相對，日光正照之，月體正受之，人目正視之。若于此際經度相及，適及兩交，日與地與月亦為一線相參直，而地在日與月之間，地既暗體，以其半體受光于日，以其半體射景于月。若月體全入于景中，則純為晦魄，必待出于景際，然後蘇而生明，如沒而復出者然。是則可謂真食也。總之日月兩曜，若同行一道之上，則每朔每望無不食矣。日月、地三體，若并不居一直線，則永無食矣。惟各行於一道，時及於兩交，故日與月皆隔五月而一食，或六月而一食。歲歲大率有之。不食者半食於夜，日食則此方所見，他方所不見耳。其食也，日體恆居一直線之此界，其彼界則月體地體疊居焉。月居末界，即月面之日光食於地景矣。「地居末界」，即地面之日光食於月景矣。

　　日月交食總圖

　　

　　日月交食總圖說

　　如上圖，「甲」為地，巳為日，卯辰圈為黃道，乙丙為白道，其大距：〈兩距之最遠〉《五》度弱。〈二分〉丁戊為兩交。〈即龍頭龍尾亦名羅㬋計都〉論《月食》：「日照地球，其光自庚辛至地切兩旁過之，而復合于壬。自甲至壬角體之形為地景。地景之心，恆隨太陽而行。黃道中線若躔處去兩交遠，二徑折半小于兩道之距度分，月行本道，從旁相過，不能逮及，則不食矣。若正遇于兩交，或交之左右，二徑折半大于二道之距度分，則兩相涉入，月為之食。其食分多」寡在距度廣狹，距度廣狹在去交遠近也。論日食則人目所見，恆在地面，推得實會，仍須推其視會，若僅據實會，則是地心之見食，非地面之見食。凡有無多寡，加時先後，悉皆乖失矣。如《圖丁》為月，或正居于兩交，或在交之左右，日月二徑之各半，合之小于距度分，則月能掩日，日為之食，不然則不食也。所謂「實會、視會兼推則合」者，地面所見，推食于地平以上，至天頂之正中，則獨推實會，便為視會。自此以外，地面所見，先後大小遲疾漸次不同。如圖人在地面，癸依丁月之徑，適滿太陽之庚辛徑，則見為全食。若人在地面，子依丁月之徑，乃見兩切線所至為己寅，則月掩太陽，止于己庚，半徑見為半食矣。大凡日欲食時，月不能離躔道一度強。自此以上，無緣相涉，故定朔之日，有食時少，無食時多也。

　　太陽本行圖

　　

　　太陽本行圖說

　　甲為地球在天心，其大小之比例，難可計算。略言之，則地之與天，若尺土之與大地也。如圖外大圈為黃道，與地同心；內圈為太陽本天，其心在乙，乙之離地心依第谷算，為全數十萬分之三千五百八十四，約之為百分之三有半也。其最高今時在鶉首宮六度為丙，太陽右行，從辛過丙，一周天而復于辛，為三百六十五日二十三刻三分四十八秒，是謂「歲實。」《任》躔某宮某度分，皆以地心甲為主，而地心所出直線，至戊黃道，指為太陽之實行。其平行則又以本圈之乙心為主。故人在地所測之實行，時速時遲。而太陽因最高在北任分，本圈則北為大半。故北六宮之日數，多於南六宮幾八日有奇也。

　　依此見求太陽之躔度必用兩法：一者定其本行，如隨乙丁己直線窺之，從乙心見黃道上之己點；二者定其實行，如隨甲丁戊窺之，乃從地心見黃道上之戊點。先得其平行，又以加減求實行，而平實之差為戊巳弧，以甲丁乙三角形求之，即得也。其自丙過秋分至庚兩行之差，必減平行而得實行。自庚過辛春分至丙，則加于平行而得實行。若用表，則從丙最高起算，或從庚最庳起算。至日體之本度為引數，以求加減之度。

　　太陰朔朢本行圖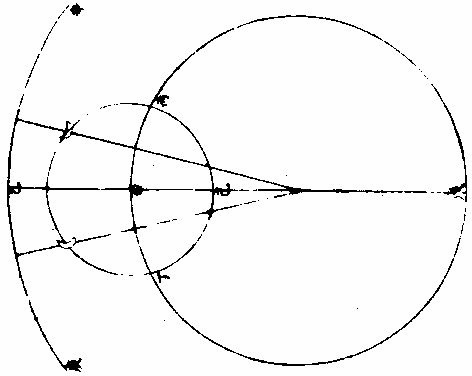

　　

　　《太陰朔朢本行圖說》：

　　月離之術，依《歌》《白泥論》，有本圜，有本輪，有次輪。本輪之心依本圈之邊滿一轉，即次輪之心依本輪之邊得兩轉，故朔朢時月體皆在次輪之最近。最近者，近於本輪之心也。因是不用次輪，但以最近處為界，得圓圈。《月離曆指》謂為本輪之內圈，此可名朔朢之小輪也。

　　假如丙丁戊為太陰朔朢時之本圈，則與地同心。〈因無差故設為同心〉本輪為乙、丙、丁，其心在本圜之邊。甲右距日得每日十二度一十一分，其最高在乙，最庳在己。月體又居次輪之邊，左行自乙至丙而己而丁，謂之「引數。」最外有黃道為辛、庚。若從地心出直線上至黃道，而次輪心正居此線之上，則所指者為太陰之平行度分也。又從地心出直線上至黃道，而月體正居此線之上，則所指者為太陰實行度分也。凡月轉或在高、或在庳，正當一宮初度；〈乙也〉或「七宮初度。」〈己也〉則平行即是實行，過此必有兩行之差。則以差數加減于平行度分，得其實行度分。又月在乙丙己半轉，則以減得之，若在己丁乙半轉，則以加得之，以在朔朢。故平實行相距之極大差不過四度五十八分二十七秒。

　　〈甲丙甲丁是也〉過此為兩弦之差，則更少與交食，無與月離。

　　曆詳之，若用不同心圈論，則并不用此本輪。其加減平行度分而得實行度分，理則一也○。因日月以平實分本行，故平朔、平朢時，兩體未必正相合、正相對，凡實會之，或先或後，日月各以其平行直線相遇，而合為一直線，則是中會。

　　實會中會視會

　　《測天約說》言「日月之行有隅照。」〈相距三之一〉有方照：〈相距四之一〉有六合照。〈相距六之一〉然悉無交食，而獨相會。〈朔也亦名合會〉相對。〈朢也亦名照會〉則能有食。故本篇所論者，止于「相會」「相對」也。抑會者，總名也。細言之，有實會，有中會，有視會，三者皆為推步之原。故言交食之術，必先言相會相對，言相會相對之理，必從「實會」「中會」始。

　　實會中會以地心為主

　　實會者，以地心所出直線上至黃道者為主，而日月五星兩居此線之上，則實會也。即南北相距，非同一點，而總在此線正對之過黃極圈，亦為實會。蓋過黃極圈者，過黃道之兩極而交會于黃道，分黃道為四直角者也。則從旁視之，雖地心各出一線，南北異緯，從黃極視之，即見地心所出二線，東西同經，是南北正對如一線也，是故謂之「實會。」若月與五星各居其本輪之周，地心所出線上至黃道，而兩本輪之心俱當此線之上，則為月與五星之中會。日無本輪，本行圈與地為不同心，兩心所出則有兩線，此兩線者若為平行線，而月本輪之心正居地心線上，則是日與月之中會也。蓋《實會》既以地心線射太陰之體為主，則此地心線過小輪之心，謂之「中會」矣。若以不同心圈之平行線論之，因日月各有本圈，即本圈心皆與地心。〈即黃道心〉有相距之度分，即日月循各本圈之周，右行所過黃道經度，必時時有差。〈與地不同心故也〉「其從地心出直線，過日月之體上至黃道，此所指者為日月之實行度分也。設從地心更出一平行直線，與本圈心所出直線偕平行而上至黃道，此所指者為日月之平行度分也。」蓋太陽心線與地心一線平行，太陰心線亦與地心一線平行，恆時多不相遇。至相遇時，兩地心線合為一線，則是日月之中相會。若太陽實行之直線與太陰實行之直線合為一線，則是日月之實相會。合會、「望會」，皆有中有實，其理不異。

　　實會中會圖二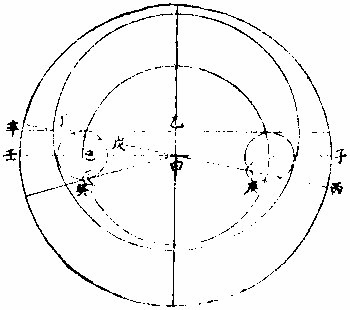

　　

　　實會中會圖說

　　先依小輪法作圖甲，為地心，亦為黃道心，亦為太陰本圈心。〈太陰與地同心者為用本輪故蓋本輪周即太陰圈心繞地心之周其理一也〉乙為太陽本圈心。〈與地不同心〉「太陽在丁，太陰在戊」，甲戊丁線直至黃道圈得辛，指日月實相會之度。如太陽在丁，太陰亦在甲辛直線上為庚，而此線至黃道圈得丙，即指日月實相朢之度。若太陰在癸，與太陽不同一線之上，乃過月本輪之心己而至黃道壬，此直線所指，則日月中相會之度也。如月在庚，從地心出平行線，甲子與甲壬太陽平行為一線，而至黃道，子亦指日月中相朢之度矣。

　　次依不同心圈法，如後圖黃道與太陽之本圈皆同前，獨太陰無本輪而易為本圈，其心與地心不同，在甲乃在丙，此亦以日月並居一直線為實會。如太陽在丁，太陰在本圈之邊戊，地心所出甲戊，丁線至辛，則所指為實會。而正對月體，至黃道寅，則所指為實朢。若中會中朢則以平行線為主。蓋甲壬為地心所「出直線，既偕太陽本圈心所出過日體之直線，乙丁為平行線，又偕太陰本圈心所出過月體之直線，丙庚為平行線」，則是兩偕行之直線合為一，甲壬而至黃道，故所指者為日月中相會之度也。其至相對之黃道上為癸，則所指者為日月中相朢之度。設過此交會之時，太陰在丑，則月圈心出者為丙丑線，地心出者為甲己線；兩線自偕為平行，而甲壬與乙丁自偕為平行，甲壬甲己不得合為一線矣。故地心所出之兩偕行線，能合為一甲壬者，必指中交之度，為日月相會之共界也。

　　《見食隨地異時》

　　月食分數，天下皆同，第見食時刻隨地各異，何也？人各就所居之地，目力所及者，則見月食，而各所居地皆以子午正線為主，若其地同居一子午線者。〈南北地緯雖異東西地經則同〉「則所見月食之分數遲速皆同也。若地易子午線易，則時刻并易矣。所以然者，時刻早晚，因太陽行度隨人所居，各以見日出入為東西、為卯酉，即以日中為南為子午，而平分時刻。故月食時必本地之日未東升或已西沉，乃得見之。若在其晝，時刻不可得見也。天啟三年九月十五夜朢，月食順天府及南北同經之地，則初虧在酉初一刻一十二分，食甚在戌初初刻，復圓在戌正二刻一十三分，各筭外。」高麗及其同經之地，即初虧在酉末戌初。而西洋意大里亞諸國，日尚在天頂為午正，則不見月食。以里差推之，西洋之初虧在巳正三刻四分，食甚在午正一刻七分，復圓在未初三刻一十分，各算外。雖月入景七分五十六秒，所居宮度彼此遠近皆同，而以里差，故彼地彼時太陽在午正二十二分，太陰反在子正二十二分，食甚正在日中，何從見之？今壬申年九月十五日夜望月食，初虧在卯初三刻，則陝西、四川等處得見，南京、山東等近海東境不可得見也。秦、蜀之子午，異于東方之子午，故

　　今以順天府推算本食，因定各省直之食時，宜先定各省直視順天子午線之里差幾何，後以其所差度數化為所差時刻。每一度應得時四分，向東以加，于順天推定時刻，向西則減，乃可得各省直見食時刻也。若日食，則其食分多寡、加時早晚，皆係視差，東西南北，悉無同者。必須隨地考北極高下，差其距度，隨地測子午正線，差其經度，乃可定其目見器測之視時。定子午術，見《西測食略》。中法于當身所居目見器測考定一月食之時刻，與先所定他方之月食時刻較算。或兩地兩人同測一月食，彼此較算，乃以所差時刻得所差度分也。

　　「前順天府所推月食時刻，并具各省直先後差數，因未得諸方見食確數，無從遽定地之經度，但依《廣輿圖》計里畫方之法，略率開載耳。」既而咨報多相合者，然非甄明之輩躬至其地，測極高下，見食早晚，終未敢以耳聞臆斷，勒為成書也。左方所記，政所謂略率開載者，欲求決定，當竢異日，故稱約加約減焉。

　　南京應天府及福建福州府約加四分〈凡一十五分為一刻〉山東濟南府約加五分。

　　山西太原府，約減一刻〇九分。
　　湖廣武昌府、河南開封府約減一刻。
　　陝西西安府、廣西桂林府，約減二刻〇四分。
　　浙江《杭州府》約加十二分。
　　江西南昌府約減一十分。

　　廣東《廣州府》，約減一刻〇五分。
　　四川成都府，約減三刻〇七分。
　　貴州貴陽府約減二刻〇八分。
　　雲南，雲南府約減四刻〇八分。

梦远书城(guxuo.com)