职业心理学第二章个性差异之量度

第二章个性差异之量度

　　吾人既已研究个性差异之原因，为研究职业心理学之背景，请再进而研究如何量度个性差异之程度。

　　量度个性差异之必要　吾人诚欲应用研究个性所得之结果，则在理论与实施各方面，对于一群内某种特性，或几种特性，皆须求得一种量度之方法。而且有时不但量度而已，并须比较各种特性。诚欲从事比较，苟仅知某人所得关于某种特性之测验分数较一群中之“平均”或“中数”多若干分，或少若干分；而未知此一群中各人测验分数之差别情形，则此人在此一群中所处之地位（指程度），仍无明确之表示也。试举一例以明之。例如此一群中受同一测验者有百分之五十，其所得之分数与“平均”比较之数，皆与此人所得之比较结果相似，则此人之程度不能有所超出。如此一群中仅有百分之五，所有与“平均”比较之数，与此人相似，则此人之程度即可视为超越矣。除此之外，关于量度个性，尚有一种需要，即尚须应用明确的方法，求出所谓“集中趋势”（central tendency）（即测验法中所称“平均”mean“中数”median或“众数”mode）之“可靠性”（reliability）。如所测验之个性愈有变异，则所测验之人数当愈多，始能获得满意之标准或“平均”。

　　关于量度某种个性之差异程度，已有数法最常用者，兹略述其概要如左：

　　（1）次数分配曲线（frequency curve）　所谓次数分配曲线，例如下图：平线代表全距离分数，由左向右，起自最低之分数，依次向右，结以最高之分数（此种种分数即由测验一群儿童某种能力所得之结果）。在平线中每一分数之上，可依得此一级分数人数之多寡，根据所定之单位（如以一人为一单位之类），记一点。俟各点记毕，以一曲线连之，即成所谓次数分配曲线。此图之功用，在能用图表示分数之分配大概，由此得觇个性差异之大略情形。如吾人已测验某人所得之分数，则察视此种曲线，一望而知此人在本群中所居之程度地位。就严格言之，此法尚不能称为明确的量度，惟以其能藉图画表明分数分配之大概，用之者颇多，尤以人数在“平均”分数以上或以下者较多时更为有用。

　　职业心理学

　　上图所示之曲线，乃一种“常态分配”（normal distribution），盖此图左右非常均匀也。受测验之人数愈多，则此种曲线愈近常态。如所得之曲线左右差池不均，称为“偏态分配”（skewed distribution）。

　　（2）全距离分数（range of scores）　所谓全距离分数，即是从最小分数至数最大分数之距离。有时欲知所测验之全群成绩，仅须叙述全距离分数，即可知其中有无甚大之差异，并可知此群所具之大概程度。核算时，只须从最大分数内减去最小分数。惟此只能作为一种参考之量数，亦非精确之量度也。

　　（3）二十五分差距离（semi-inter-quartile range）　较全距离分数更准确者为二十五分差距离，包含全体分数之中间50％，除去最高分数之四分之一与最低分数之四分之一。此法可表明全群中成绩之中间一部分，占全部分之一半。如以Q代二十五分差，其核算之公式如左：

　　

　　公式中之Q1系代表下二十五分点，为一种点数，在此点数以下有全体分数之25％，在此点数以上有全体分数之75％。Q3系代表上二十五分点，亦为一种点数，在此点数以上有全体分数之25％，在此点数以下有全体分数之75％。

　　（4）平均差（average deviation, A. D. , or mean deviation, Mn. D.）　就严格言之，上述之三法，其功用只能作为一种参考的量数；若“平均差”则比较的更为明确之量数矣。然平均差尚属明确量数之最简单者，乃计算“均方差” （standard deviation）或“机误”（probable error）之第一步也。所谓平均差，盖指个人所得之分数与一群中之平均或中数比较之平均差数。其核算方法如左：（差数之正负号不计）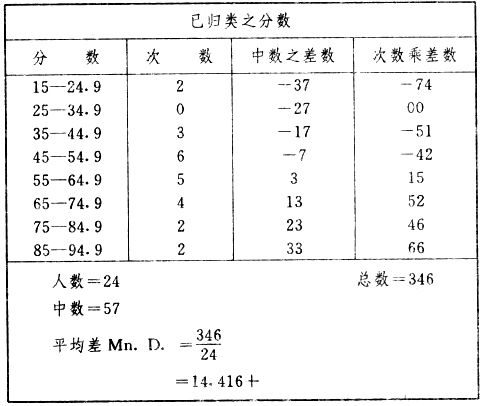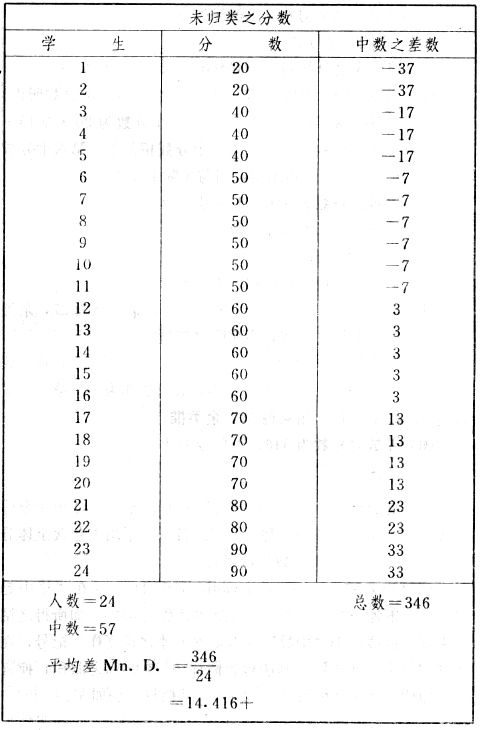

　　职业心理学

　　兹再将上述之平均差算法解释如左。

　　（甲）未归类之分数：

　　（a）将原来之分数列成顺序分配。（此一步可省）

　　（b）人数＝24，中数为57。（中数系由2除分数总数所得）

　　（c）求各分数与中数之差数。第一个分数为20（为15－24.9之中点）与中数相差37，第三个分数相差17，第六个分数相差7，余类推。负号可不用，因与实际上无关系。

　　（d）差数之总数为346，正负号不计。

　　（e）平均差等于人数除差数之总数。

　　（乙）已归类之分数：

　　（a）将原来差数重行排列，求次数分配。

　　（b）第一级15－24.9之离中差为37，第二级为27，余类推。此差数并非级之差数，乃实际之差数。

　　（c）次数乘差数。例如第一级之次数有2，故用2，乘差数37，总数为74。第二级之次数为零，故总数亦为零。第三级次数为3，差数为17，相乘得51，余类推。

　　（d）差数之总数为346，正负号不计。

　　（e）平均差＝346／24=14.416+

　　就常态分配言，在“集中趋势”上下之各一个Q包含全体分数之50％，在“集中趋势”上下之各一个平均差包含全体分数之57.5％，故后者之数较前者为大。

　　（5）均方差（standard deviation, S. D.）　在“集中趋势”之上下各一个均方差，约占全体分数之68％。如所得之结果系常态曲线，于“中数”左右依均方差之长度作一记号，在此两记号上画两垂线，则能包含曲线内68.26％之面积，换言之，即能包括全体分数之68.26％。其核算方法如左：

　　职业心理学

　　兹再将上述之均方差算法解释如左：

　　（甲）未归类之分数：

　　（a）将原来之分数列成顺序分配。（此一步可省）

　　（b）人数＝24，平均数为7.0。因欲免除差数之小数，故用假定的平均数7.5代替平均数7.0。如不用7.5，用9.5或2.5均可。（平均数7.0系用人数除分数总数所得，所以须加.5，因2分实际为2－2.999中点为2.5）。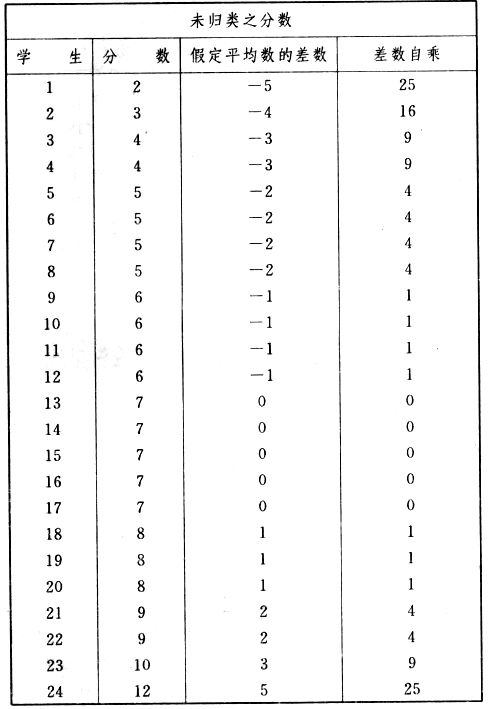

　　职业心理学

　　（c）求各分数与假定的平均数之差数。第一个分数为2，实际为2－2.99，中点为2.5，与假定之平均数相差为5。余类推。

　　（d）各差数均自乘。

　　（e）差数方之总数为124。

　　（f）均方差S. D. 为人数除差数方之总数，减去校正数的方之方根。校正数的平均数与假定的平均数之差数，在此例内为.5。

　　均方差S.D.= 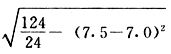职业心理学

　　（乙）已归类之分数：

　　（a）将原来分数，重行排列，求次数分配。

　　（b）人数＝24，平均数＝7。

　　（c）将接近分配中央任何一级之中点，用为“参照点”。凡用假定的平均数，皆取一级的中点。假定的平均数为7.5。

　　（d）求各级与假定平均数之差数。

　　（e）差数自乘，再乘次数。从上边乘起：（5）2×1＝25，（4）2×1＝16，（3）2×2＝18。余类推。

　　（f）均方差S.D.= 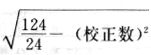职业心理学

平均数与真实的平均数之差数，在此例内为.5。倘遇无差数，则校正数为零。所以须用假定的平均数，再行校正，盖欲便于核算计，免除小数搀入。

　　（6）机误（probable error, P. E.）　所谓机误，亦与分配曲线图有关系。此指量表上（即分配图之底线）之一种距离单位；如在“中数”左右，依机误之距（即长度）作记号，即可表明曲线内全部面积之50％，换言之，即包含全体分数之50％。其算法只须将.6745乘均方差S.D.即得。其公式如左：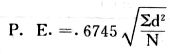

　　职业心理学

　　公式中之d指中数之差数，∑指总数，N指人数。

　　左列一表，表示依据以P. E. 为单位离开“平均”之远近，其所包含之全体分数中百分之几亦因之而异。惟此表仅限于常态次数曲线。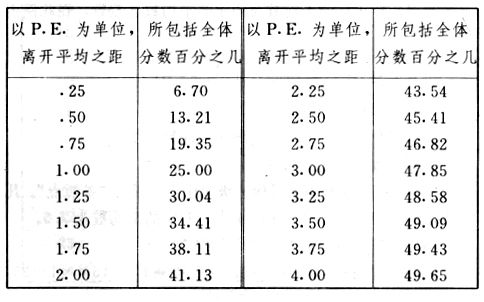

　　职业心理学

　　以上所述可得核算之各种方法，皆以数目字表明在“量表”上与“平均”相离之“距”，藉此表明一级或一群中个性差异之大概趋势。此数法皆应用统计学于教育方面者也。此外统计学中尚有一法与个性差异之量度亦有重要之关系，即所谓相关度。

　　相关度之创始　相关度创自葛尔顿（Galton），葛尔顿研究遗传，需要此种量度方法，故此事之探讨，由彼开其端焉。关于相关度之进化史与其公式之沿革，其详情非本章范围所及。惟“相关系数”（coefficient of correlation）在心理学、教育学、经济学等等专门科学中皆有甚大之贡献，尤为研究个性者所不可不知，故其功用与核算方法，为研究职业心理学者所宜特加致意。

　　相关度之意义　所谓相关度，乃一种方法，用以鉴定一组人，或一组学校，或其他团体，其所有之两种成绩间有何连带关系？如两种之间有绝对之正比例关系，相关系数（r）为+1.0；如两种之间仅有反比例之关系，则相关系数为-1.0。如两种成绩彼此间毫无关系，则相关系数为0。据经验所示，自0至±.4相关为低；自±.4至±.7之相关颇有关系；自±.7至±1.0之相关程度为高者。

　　相关度在教育方面之功用　相关度在教育方面之功用甚大。吾人所采用之智力测验或教育测验，其结果是否可恃？教师之评判与测验之等第是否相符？各种能力彼此间有否连带关系？各种智力与各种科目彼此间是否有连带关系？学业成绩与实际事业之成功有多大关系？此类问题之答案，皆得以相关度之方法解决之。

　　核算相关度之方法　现今最通行之核算相关度方法，皆用潘阿生（Pearson）所创作之公式：

　　

　　公式中之r指相关系数，∑指总数；x指第一组测验分数与平均数之差数，y指第二组测验分数与平均数之差数；N指人数；σx指第一组测验之均方差，σy指第二组测验之均方差。上述公式亦可列成如左之公式：

　　

　　兹举一例如左，说明用此公式核算相关度之方法：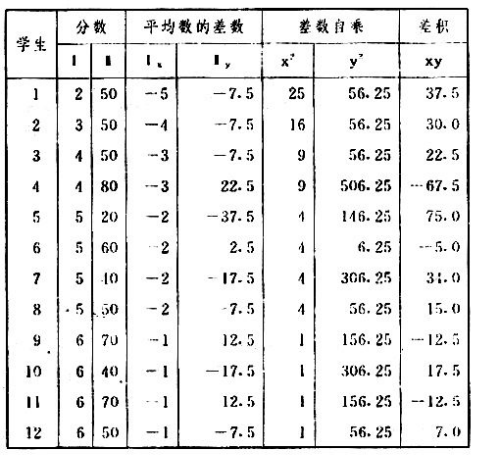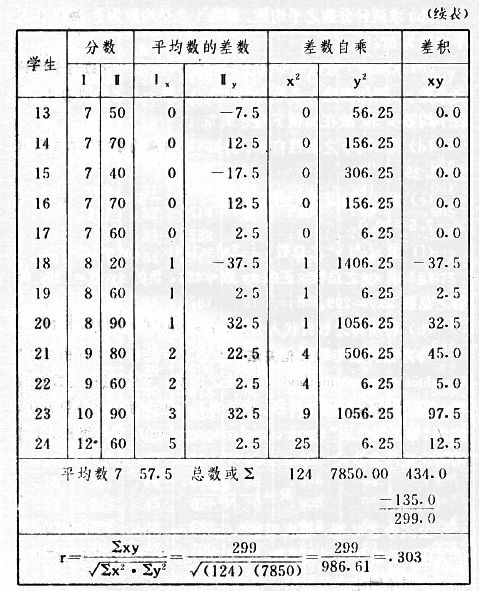

　　职业心理学

　　兹将上表所示相关系数核算法说明如左：

　　（a）依各人之号数，将两种测验之分数依次排列，例如第一人所得测验Ⅰ之分数为2，所得测验Ⅱ之分数为50。余类推。

　　（b）求两种分数之平均数。测验Ⅰ之平均数为7，测验Ⅱ之平均数为57.5。

　　（c）求测验Ⅰ分数与平均数之差数x，测验Ⅱ分数与平均数之差数y。例如测验Ⅰ之平均数为7.0，第一人之分数为2，比较平均数少5，故在x项下写一负5。

　　（d）将x与y之数目自乘。例如-5自乘为25。-7.5自乘为56.25。

　　（e）求x与y之相乘数。例如-7.5×-5＝37.5。又如-4×-7.5＝30.0。

　　（f）求x2与y2之总数　　∑x2＝124　　∑y2＝7850

　　（g）求xy之总数。正的xy数＝434，负的xy数＝135。两数之总数∑xy＝299。

　　（h）将所得之数目代入公式，r＝.303

　　均方相关法与等级相关法　上述之方法系“均方相关法”（product-moment method），此法之核算，可不用相关数对数表，其结果比较的最为可靠。此外尚有一更为便利之核算方法，称为“等级相关法”（rank correlation method）。求等级相关，可用斯比亚门之公式（Spearman "Footrule" Formula）：

　　

　　公式中之G指“名次较数”（gains in rank），∑指总数，N指人数，R指名次相关系数。用上列公式得到“名次较数”后，尚须参照潘阿生之对数表，化成相关系数。

　　核算相关度之对数表　化R为r之对数表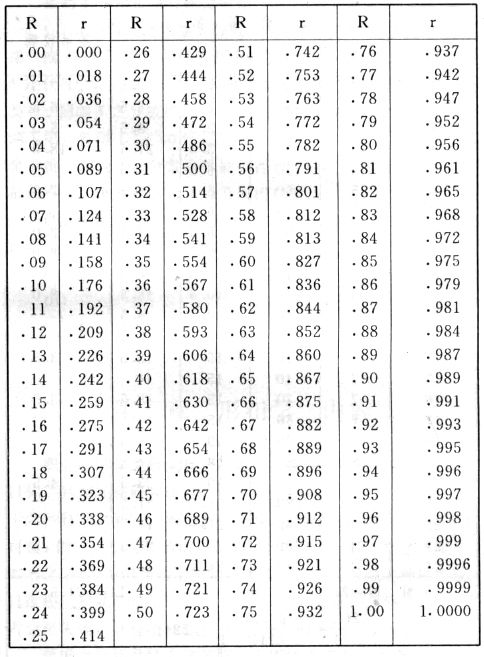

　　

　　既有此表，请再举一例，以示等级相关之核算法：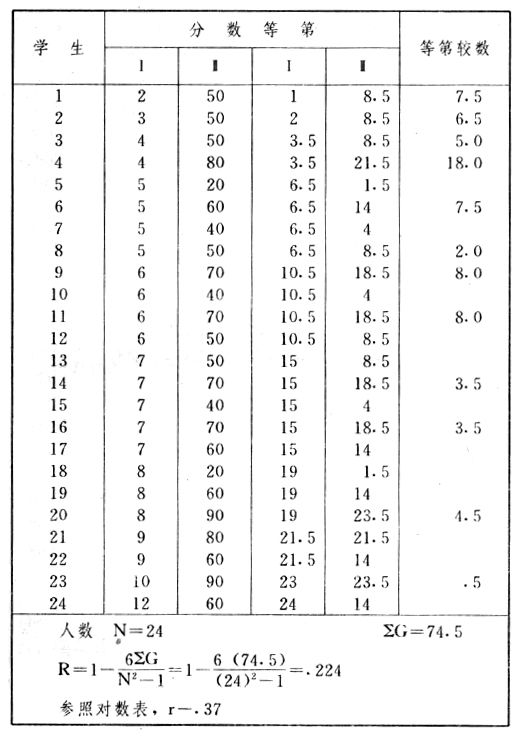

　　职业心理学

　　兹将上述用表核算法说明如左：

　　（a）先将各人之测验Ⅰ分数，列成比较的等第。例如2分列第一或1；3分列2；4分有两个，平分3、4等第，故各列3.5；5分有四个，将5、6、7、8四个等第平均之后，各得6.5；余类推。测验Ⅱ之分数亦列成等第。例如20分有两个，平均1、2两等第，各得1.5；40分有三个，平均3、4、5等第，各得4；余类推。测验Ⅰ之分数系以量小者列在最前，如以最大者列在最前亦可，惟两种测验之等第须相对照。

　　（b）核算超过第一次等第之数，获得等第较数。例如8.5-1=7.5；8.5-2=6.5。余类推。

　　（c）求得等第较数之总数。∑G=74.5

　　（d）代入公式，R=.224，参照对数表化成r，r=.37

梦远书城(guxuo.com)