| 梦远书城 > 类书 > 古今圖書集成·乾象典 | 上页 下页 |
| 第二十五卷 |
|
|
|
七政部彙考二 《明陽瑪諾天問略》 《天有幾重及七政本位問答》 問:「人居地上,依其目力所及,獨見一重,自東而西,一日一周耳。今設十二重,何徵?」曰:「萬物或靜或動,靜者獨有一靜,是靜無動;動者獨有一動,是動無靜。終古以來,未有一息之內,能動靜互現者也。未有二動並出,能此動東去,彼動西行者也。於其運動相反,可知其體有同異矣。今恆見日月五星列宿,其運動各各」相反,便知所麗之天,原非一重。日月相反運動,於朔朢見之。「朔日月共躔一度,朢日月相遠半周。」月每日自西而東,行十三度有奇,日每日約行一度。五星所離日月列宿,每日各異,其相近相遠,亦各時刻不同。 因知各有其本重所麗之天,可證五星之有五重天也。列宿諸星,相近相遠,終古恆同,因知其所麗天終古恆同,而可證其有第八重天也。夫日月諸星本動之天,皆自西而東也。天左旋,日月五星右行,貴國先儒亦已晰之矣。今舉目而視之,日生於東,沒於西,月與諸星隨之以旋,其自東而西者又昭眧然。此必有一天焉,為之主宰,為之牽屬,而日月諸星之天因之,則九重天是也。故自「東而西」者,宗動天也;「自西而東」者,日月諸星之天也;「自西而東」者,日月諸星之本動也;「自東而西」者,日月諸星之帶動也。明乎二動,得天體也。第九第十重天,其說甚長,宜有專書備論。 十二重天圖  十二重天圖說 問:「既有十二重天,敢問太陽何位?」曰:「自下往上,在第四位,七政之中也。日得其中,為其本所,光及餘政,暄及下地故也。為其本所者,七政之中,日最貴尊。貴尊之物,得其中位,一定之勢也。光及餘政者,是月無光,恆借日之光以為光。試觀月之於日,合則魄,遠則弦,對則朢,隨其近遠,以為明闇焉。五星列宿,亦復如是。」蓋日居其中,適得上下照映也。「暄及下地」者,日光在中,下濟萬物,氣以暄之,乃得調和。若居最上,則溫煖不及,諸物難以滋生,若居最下,則燥熱太甚,諸物受其暵損。故日得中正。中和之理,萬物之宜也。諸天本位,可視右圖。 土星圖 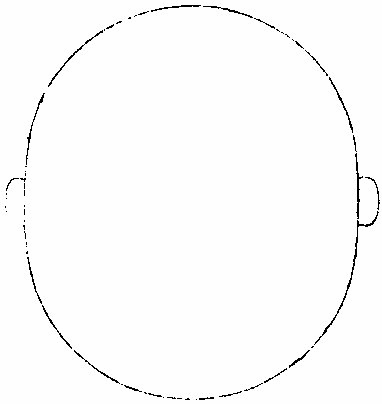 土星圖說 觀土星,則其形如右圖,圓似雞卵,兩側繼有兩小星,其或與本星聯體否?不可明測也。觀木星,其四圍恆有四小星,周行甚疾,或此東而彼西,或此西而彼東,或俱東俱西,但其行動與二十八宿甚異。此星必居七政之內,別一星也。 《羅雅谷五緯曆指》 《周天各曜序次》 周天諸曜,位置有高庳,包函有內外,去人有遠近。何繇知之?以其相食、相掩知之。凡相食、相掩必參相直,參相直必分三界。人目為此界,所食所掩為彼界,則食之掩之者,必在其中界也。 第一最近為太陰,太陰在食日能掩他星,他星不能掩太陰。第二為水星,第三為金星,第四為太陽,第五為火星,第六為木星,第七為土星,第八為恆星,第九為《宗動。天中世》于恆星天上,又增東西歲差一天,南北歲差一天,共為十一重天。 《恆星本天》,在《七曜天》之上,古今諸家之公論也。試法有三: 其一,緯星能掩恆星,恆星不能掩緯星。 如唐高宗永徽三年正月丁亥,「歲星掩太微上將」 ;「正月戊子,熒惑掩右執法。」 元武宗至大元年十一月戊寅,「太白掩建星」 之類。 其二,緯星有地半徑之差,各去地有遠近,而差有多寡。恆星古今密測,絕無地半徑差,則以較緯星必為極遠、極高,其視地球正為一點。 其三為恆星。天之本行極遲,則當為極高極遠。 《解》曰:「諸星行,天之能力必等,行力既等,而各所見之本行有遲有疾,必所行之軌道有大有小故也。月天甚近,於地甚小,故二十七日有奇而行一周,恆星必六十餘年而行一度,甚遲必甚大甚遠矣。三者相因之勢也。」〈因此論亦得諸星相距之高庳〉 太陽在諸曜適中之處,亦古今無疑。《試法》有四,其一「諸星受光於太陽,若在甚高或甚庳,即不能平分其光。又太陽為萬光之原,其在眾星之中,若君主在眾臣之中。」 其二,日躔月離各《曆指》測算,太陽距地之遠為地半徑者一千一百個有奇,太陰距地之遠六十個有奇,則月天與日天相距當一千個有奇,其間不應空然無物,會當有星,則金水兩星之天在其中矣。若此外,土木火三星其行甚遲,其所行本天甚大,故非日月兩天之間所能容受也。 其三,「諸星之視差與地半徑差各各不等。太陽之兩差,不能多于太陰,太白不能少于木星,土星則當在其中處。」 其四。中西曆家所立法數,種種不同。其同者有二:「一、周天分二十八宿,其距星合者二十七,不合者獨觜宿耳;二、以七政隸于各日。初日為太陽日,次為太陰日三為水星,日四為火星,日五為木星,日六為金星,日七為土星日也。夫七政自上而下,當首日,次金、水、月、土、木、火。今云然者,日分二十四時,七政分屬焉,周而復始。今所指直日者,各日之首時也。如初日之首時,為太陽時,次金星時;三、水星時,四、太陰時,五、土星時;六、木星時,七、火星時。滿二十四時為水星,則次日之首時為太陰矣。故太陽之次日,即為太陰之日。可見上古曆宗初立此法者,知太陽在眾星之中處也。」上三論,古今無疑。其不同者,古曰五「星之行,皆以地心為本天之心,今曰五星以太陽之體為心。」古曰「各星自有本天,重重包裹,不能相通,而天體皆為實體;今曰諸圈能相入即能相通,不得為實體。古曰土木火星恆居太陽之外,今曰火星有時在太陽之內。」解曰:「用遠鏡見金星,如月有晦朔弦望,必有時在太陽之上,有時在下,又火」星獨對衝太陽時,其體大,其視差較太陽為大,則此時庳于太陽。水星、木星、土星,不能以正論定其高庳,但以遲行疾行聊可證之。 七政序次古圖 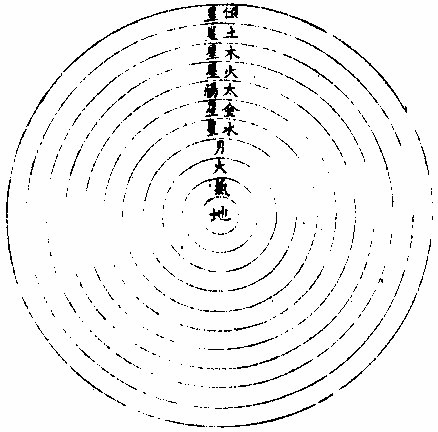 七政序次古圖說 古圖中心為諸天及地球之心第一小圈,內函容地球,水附焉。次氣、次火,是為「四元行。」月圈以上各有本名,各星本天中又有不同,心圈有小輪。因論天為實體,不相通而相切。 七政序次新圖 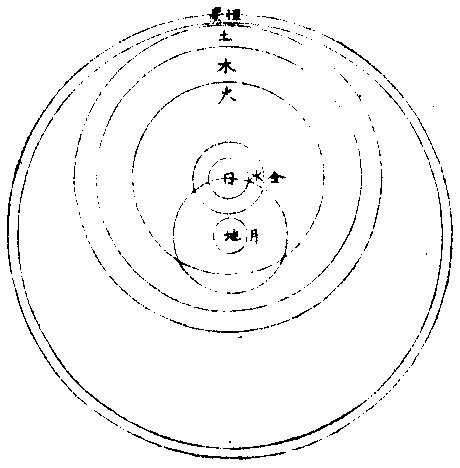 七政序次新圖說 《新圖》則地球居中,其心為日月恆星三天之心。又日為心,作兩小圈,為金星、水星。兩天又一大圈稍截太陽本天之圈,為火星天。其外又作兩大圈,為木星之天、土星之天。此圖圈數與古圖天數等,第論五星行度,其法不一。 依《新圖》可見金星以太陽為本,天之心,在上則得全光,在下則無光也。又可見火星對衝太陽時,則庳于太陽,皆與所見所測合。又金水二星,以太陽之平行為本。天之平行,古今不異,則三天之行,皆繇一能動之力,此能力在太陽之體中也。 問:「金、水二星既在日下,何不能食日?」曰:「太陽之光,大于金、水之光甚遠,其在日體不過一點,是豈目力所及?如用遠鏡如法映照,乃得見之?依本測法,太陽之面大于太白之面一百餘倍,辰星尤微。」 問古者諸家,曰天體為堅為實,為徹照今法火星圈割太陽之圈,得非明背昔賢之成法乎?曰:「自古以來,測候所急,追天為本,必所造之法,與密測所得,略無乖爽,乃為正法。苟為不然,安得泥古而違天乎?以事理論之,大抵古測稍粗,又以目所見為準則更粗。今測較古,其精十倍,又用遠鏡為準,其精百倍,是以舍」古從今。良非自作聰明。妄違迪哲。 問:「金水二星,其孰上孰下?何從知之?」曰:「水星之天,小于金星之天,知水星必在其內。」 《水星》左右距日二十餘度,金星左右距日四十餘度。 又曰:「太白行遲于水星之行,則其軌道必大。」 金星次行,約二十月而一周,水星次行,約四月而一周。 問:「金星居兩留段時,即與弦月不異,辰星豈不當爾乎?」曰:「論理宜然。特因體小,出沒必于晨昏難見,故未覺其盈虧消息耳。」 問「土、木、火三星孰上孰下。」曰:「火星在日之衝,其視差大于日之視差,其體亦大。密測密推,知其庳于太陽。 過此以往,其視差小于日之視差,其體亦小。推算所得,又高于太陽。若土木二星視差恆小于日,必在日上無疑也。又土木火三星行度不等,遲行者必在上,土星是也;疾行者必在下,火星是也。行在遲疾之間,則木星位置宜在火土之間矣。此三星上下古今同論。」 土星三十年一周天,木星十二年一周天,火星二年一周天。 《定五星之平行率》 測算各星平行,得數如左: 《土星》以五十九年。〈節氣或天周年〉又一日四分日之一,弱行次行圈。〈即歲行〉五十七、周〈會日五十七次對衝亦五十七次〉《行天周》,〈節氣周〉二周又一度四十三分。 木星以七十一年不及四日,又六十分日之五十四行,次行圈六十五周,此積時間星行本圈。〈天周或節氣或經度〉六周不及四度,又五十〇分。 「火星以七十九年又三日六十分日之一十六行,次行圈三十七周,經周行四十二周,又三度〇十分。」上三星之中積年數。〈太陽行全天之周數〉去減本星次行之周數,其較為星本行周天之數。如土星五十九年減次行五十七周,較二為土星行全天二周。 上三星者,「火木土」 也。下二星者,水金也。 《金星》「以八年不及二日,又六十分日之一十八行次行圈五周,其平行與太陽同。」 水星以四十六年又一日六十分日之三行,次行圈一百四十五周,平行與《太陽》同。 以積年變日,以天周化度,得數如左: 《土星》,二萬一千五百五十一日一十八分。〈日六十分下同〉行二萬〇五百二十〇度木星二萬五千九百二十七日。又三十七分,行二萬三千四百〇〇度。 火星二萬八千八百五十七日。又五十三分,行一萬三千三百二十〇度。 《金星》二千九百一十九日。又四十分行一千八百〇〇度。 水星一萬六千八百〇二日。又二十四分,行五萬二千二百〇〇度。 若以度為實,日數為法而一,得各星一日之細行。 土星一日行。〈距太陽之行〉〇度五十七,分四十三,秒四十一,微四十三,纖四十〇,芒。 木星一日行。〈距日〉五十七分〇九秒〇二微四十六纖二十六芒。 火星一日,行二十七分四十一秒四十〇微一十九纖二十〇芒五十八末。 金星一日,行三十六分五十九秒二十五微五十三纖一十一,芒二十八末。 水星一日行三度〇六分二十四秒〇六微五十九纖三十五,芒五十〇末。 若太陽一日之平行,去減各星一日之細行,其較為各星之平行,得上三星之平行。〈下二星金水之平行與大陽箏〉土星一日平行〇二分〇三秒一十三微三十一纖二十八芒五十一末。 木星一日平行 四分五十九秒一十四微二十六纖四十六芒三十一末。 火星一日平行三十一分二十六秒三十六微五十三纖五十一芒三十三末。 有一日之平行,可細推一時一分,又推得一年之平行。 土星一平年。〈三百六十五日〉行三百四十七度三十三分〇〇四十六微有奇。 木星一平年,行三百二十九度二十五分二十一秒有奇。 火星一平年,行一百六十八度二十分半有奇。 金星一,平年,行二百二十五度〇一分三十二秒有奇。 《水星》一平年,行全周外又五十三度五十六分四十二秒有奇。 又以太陽行一年之全周,去減各星之平行,其較為各星一年之經度。 土星一平年,經行十二度一十三分二十三秒五十六微有奇。 木星一平年,經行三十〇度二十〇分二十二秒五十一微有奇。 火星一平年,經行一百九十一度一十六分五十四秒二十二微有奇。 依上行數,先置曆元一數,可列向後各年及日時之立成表。 《新星解》 按古今曆學,皆以「在察璣衡、齊政授時」為本。齊之之術,推其運行、合會、交食、凌犯之屬,在之之法,則目見器測而已。然而目力有限,器理無窮。近年西土有度數名家,造為窺筩遠鏡,能視遠如近,視小如大,其理甚微,其用甚大。今述其所測,有關七政者,一二如左: 土星旁小星圖  土星旁小星圖說 「土星向來止見一星,今用遠鏡見三星,中一大星是士星之體,兩旁各一小星,係新星如圖。兩新星環行于土星之上下左右,有時不見,蓋與土星體相食。」或曰:「土星非渾圓體,兩旁有附體如鼻,以本軸運旋,故時見圓,時見長。」此土星之兩異行未定其率,蓋本周極遲,初見時至今年尚未滿一周天故也。或曰:「時見三星。相距有近有遠。安得謂之合體。」二說不同。未知孰是。須久測乃知之。 木星旁小星圖  木星旁小星圖說 「木星,目見一星」,今用遠鏡見五星。木星為心,則有四小星,常環行其上下左右,時相近,時相遠,時四星皆在一方,時一或二或三在一方,餘在他方,時一或二不見,皆用遠鏡可測之。初測者作此直線圖。其九測:一為萬曆壬子年,太陽在元枵初度辰時;二為癸丑年,太陽在元枵二十六度子正時;三為本年次日寅初三刻。四為本年太陽在娵訾二十三度亥初刻。五為次日丑正刻。六為甲寅年太陽在大梁八度亥初一刻。七為本日子初刻。八為次日子正二刻。九為本日寅初刻。依上測得其相距極近之圈半徑為木星三徑。〈用木星半徑為法葢無他物可與為比〉次小星圈半徑,為木星四徑,第三為五徑,第四為十徑。 木星順逆行圖 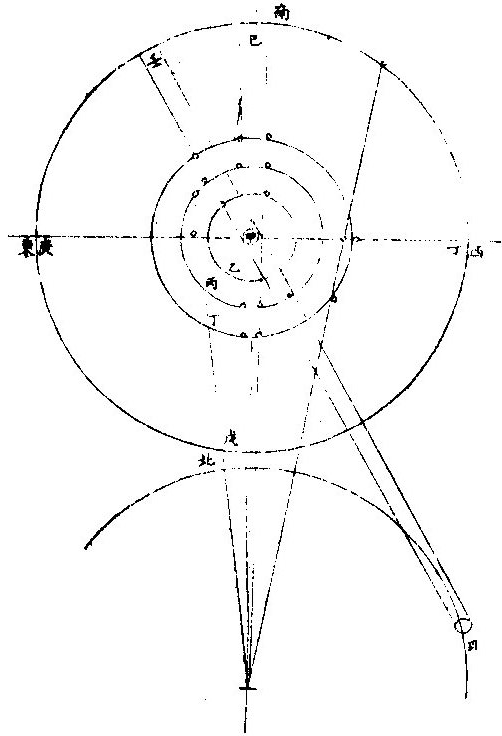 木星順逆行圖說 其行右旋,在上順行,在下逆行。〈順者自西而東逆者自東而西〉「近本星疾行,距遠遲行順行,與木星會則不見。」蓋木星食之,逆行不食,可知其環行也。又木星為其環行之心,又環行之大圈平面不與木星之本道同面,而四小星之各圈平面,又不作一大圈平面。蓋其高下不一,在高者距南,在下者距北。 次圈線圖木星甲為心,作乙丙丁戊圈,距心見上。每圈為一小星之軌道,外圈從戊向丁己庚行,餘倣此。 乙星行滿本周,為一百七十四刻,丙星行一周為三日五十三刻有奇,丁星行一周為七日十六刻,戊星行一周為十六日七十二刻弱。皆從木星會合時起算,不用距木星之極遠。葢眾星依本小輪行至左右「為留段」,不見其行,無從得真率也。 又小星在甲己左右兩線內,即隱不見,木星掩之故也。在甲壬左右兩線內,亦隱不見,蓋入木星之景故也。〈設日所在如圖照木星生甲壬景因木星距日幾何得甲壬景所在〉《今目恆見,四時見三,所不見者,必在己或壬》兩暗處。 系木星全為暗體,小星之體,亦自無光,光借于日,故入木星,景如壬,目所不見。 四、小星去木星遠,見大近,則木星光大,能奪小星之光。 問:「晨昏時比中夜見小星之光為大,何故?」曰:「晨昏之光,朦朧之光也。其光不大,故能助目之光。」 又問:「遠鏡中若少離木星之體,即不得見小星,何故日本星光助目,以能分小星之體?」已上兩言,聊以答問,未知其正理安在,俟詳求之。 《測四小星》,當于其較著時,一為木星,與日衝照。〈此時木星距地甚近〉一在本輪之最庳,一晨昏時,一月明時,金星旁無新星,特其本體。如月有朔朢,有上弦、下弦,太陽四周有多小星,用遠鏡隱映受之,每見黑子,其數、其形、其質體皆難證。《論目》以時多時寡,時有時無,體亦有大有小行,從日徑往,過來續明,不在日體之內,又不甚遠,又非空中物。此須多處多年多人密測之乃可,不關人目之謬。用器之缺。詳見《性理書》中。 又以遠鏡窺太陽。體中見明點。其光甚大。 又「日出入時,用遠鏡見,日體偏圓,非全圓也,其周如鋸齒狀。然因其行無定率,非曆家所宜詳。」亦解見《性理》。 《土星表所用諸率》 最高行一年為一分二十〇秒一十二微,一千年行二十二度一十六分四十五秒一萬六千,一百六十〇年滿一周。 平行一平年,為一十二度一十三分三十五秒二十〇微。 一日為二分〇,秒三十二微。 一時為五秒〇一微。 一萬〇七百四十七日一十八時〇,七分滿一周。〈二十九平年又一百四十二日一十八時〇七分〉 自行一年,為一十二度,一十二分,一十五秒。 《火星諸行率》 「火星最高行,一年行一分十四秒五十二微。以百年計之,行二度四分四十七秒三十二微。約千年行二十度四十七分五十六秒三十微火星平行,一日行三十一分二十七秒。以百日計之,行五十二度二十四分二十六秒。以一年三百六十五日計之,為一百九十一度十七分〇八秒。 火星滿周天之行,以前二行計之,為六百八十六日十九時。〈小時〉四十二分,十三秒。 《金星天以太陽為心》 《本曆總論》有《七政新圖》,以太陽為五緯之心,然土、木、火三星在太陽上難徵。今以金星測定,無可疑。 金星圖 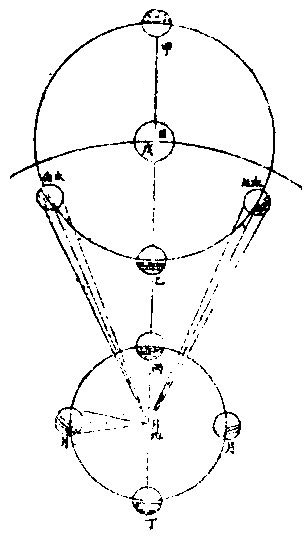 金星圖說 試測金星于西將伏、東初見時,用遠鏡窺之,必見其體,其光皆如新月之象,或西或東,光恆向日。又于西初見、東將伏時,如前法窺之,則見其光體全圓。若于其留際觀之,見其體又非全圓,而有光有魄。蓋因金星不旋地球如月體,乃得齊見其光之盈縮。故曰:「金星以太陽為心。」如圖月在太陽人目之間為丙,則無光。金星在太陽人目之間為乙,亦無光。若地在戊日丁月之間,則月光滿。若太陽戊在金星甲地球之間,則金星光滿。若在左右,則月及金星各有半光。光之大小。如按古圖,不析其理,雖千百世不能透其根也。 古者言「太白在本輪上,體小光盛,在本輪下,體大光淡,在左右體不甚大,而光甚盛。」今如圖解之,「在高」,于時為朢,其體遠則見小,全透其光,故盛也。「在庳」,于時為晦,不可得見晦朔左右去地為近,則體見「大哉生明」,故稍淡也。在左右為上下弦所見半體,故不甚大。 遠近之間,又見半光,故甚盛也。 又金星因歲輪于地時近時遠,遠時顯,其體小而光全。若以遠鏡窺之,難分別。其或圓或缺之體,在極遠左右數十度亦然。若在中距者,其光稍淡,則遠鏡可略測其體之形。然光芒銳利,亦難明別為真體。或為虛映之光。惟在極近數十度則光更淡。又于地近,其體顯大,可明見之。 凡金星為遲行或逆行,用遠鏡窺之,可測其形體。若更近見,其體缺更大。 《金星諸行率》 本天最高行,每年一分二十二秒五十七微,百年行二度十八分十六秒十二微,約一萬六千餘年而滿一周。 本天上平行,如太陽三百六十五日二十三刻有奇,而行滿一周。 小輪上之行,每日三十六分五十九秒有奇。 一、《平年》〈三百六十五日〉行七宮,十五度一分五十秒。計六百六十二日十四小時。〈不及四分〉而滿一周。 《水星本天象》 水星以太陽平行處為本行之心,即以太陽之平行為自行之平行,如金星無二,然其兩行之差,非太陽兩行之差,則必有自行本圈而載其次輪。又此圈或圈上之行非平,有高有低,與他星等,何以知其然耶?曰:「見其距太陽之大距度時有大小,因知其次輪必有遠近也。」今以《圖略》解其所測于左:〈次輪亦名伏見輪〉 水星次輪圖 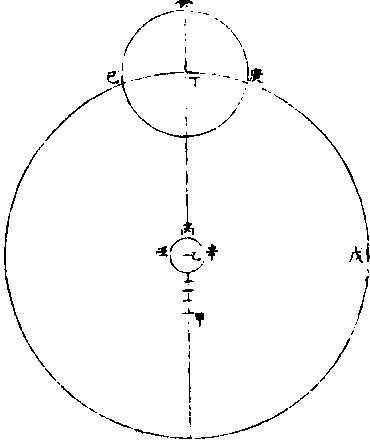 水星次輪圖說 古圖設甲為地心,任取甲乙某線分為五平行。又以乙為心,取甲乙線五分之一為半徑,作辛丙壬小圈,名曰「均圈。」又於小圈周上取丙點為心,作己丁庚戊大圈。又作甲乙丁線為兩心線,取丁點作己癸庚圈,是名「水星次輪。」 木、火、土三星名曰「歲輪」 ,金水不然。蓋以其率非滿一年,而所差復遠,故名「次輪」 ,又名「伏見輪。」 行法:甲丁線順天平行,每年一周,如太陽平行無二其自載乙點圴輪心及丁次輪或伏見輪之心,如丁心行丁庚戊本天圈,一年一周,其心在辛壬丙均輪上而行。此本天之心有行之理。獨水星如是,而他星不然,葢他星有定,兩心差之數,不加不減,故其歲輪心。〈如丁〉所行之跡亦為渾圓圈,惟水星小輪心丁所行之跡有如卵形,上寬下窄,故曰「己丁庚。」本圈之心於甲點時近時遠,又時在乙甲線內,或時在外。如置丁心在兩心線上,其行之心在辛極遠處。丁心行本天一周,必行辛壬丙小圈三次,丁心在戊最低,其行心在丙。 凡丁心在本輪上平行一周,即於小均輪上之行有三周,本輪上行一度,均輪上行三度。 以一周與三次論之,則知一度三度。 《水星平行率》 水星一小時行七分四十六秒。 一日行三度六分二十四秒。 一平年,行三全周外,五十三度五十三分三十二秒。 一閏年,三全周外,行五十七度三分五十六秒一百一十五日二十一小時三分二十二秒,行小輪一周。 《界說》 「七政凌犯,曆家恆言。顧有所以然之理,未明其理,未透其根,則測無算,難相符合。惟明其所以然,則先推後測,無弗合者。」蓋七政之行,有遲疾不等,是以後先參錯。其所呈象,約有五種: 一會聚界:會聚者,是彼此兩曜在黃道上同經度。若月于太陽曰「朔」,星于太陽曰「合」,伏星于星曰「凌」、曰犯。 《古占法》:「二星相距七十內曰犯,二星光相切曰凌。」 若經緯度俱同在日月曰「食星」於星或月於星曰「掩。」 同經度有二,或同黃道,或同赤道。在赤道同度,謂之「同升。」 此謂「同度」 ,但指黃道言也。 二、對照界。對照者,乃相距天周之半為經度。二日八十度。月對日曰「朢」,經緯俱對曰「月食」,星對日曰「夕退」,統名曰「衝照。」 月與土、木、火三星皆能於日對照,亦能各相對照。金水二星不然,蓋其不離日之左右,故於日不對。 《照亦不相對》照。 三、方照界。方照者,相距天周四之一,即九十度也。月距日曰「上下弦。」他曜相距,統名曰「方照。」 四、「隅照」界隅照者,相距天周三之一,乃一百二十度也,亦名「三角形照。」 《五六合照界》六合照者。乃相距天周六之一。即六十度也。 以上諸照視諸曜之性情,或相益,或相損,或相勝,或相和,象懸于天,而宇下徵驗因之。 五照圖 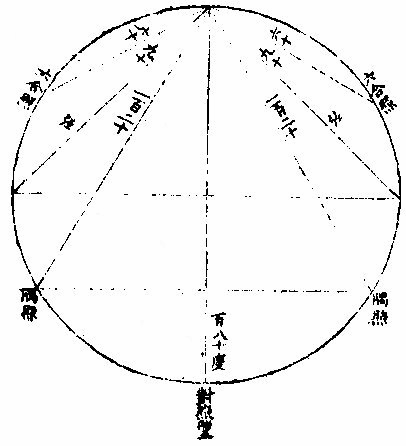 五照圖說 周圈為黃道,各分其照之界,以相距之度著其名。而照有先後,先者順天數,後者逆天數。 《諸曜伏見說》 凡星會太陽時,太陽光大,勝於星光,人目不能見星,故曰「伏。」 「夕伏」者,星比太陽行遲,合後太陽,故夕初伏不見,亦名「西伏」,如土木、火三星及金水二星逆行之時。 「晨伏」者,星比太陽行疾,合先太陽,故晨初伏不見,亦名「東伏。」 惟金、水二星及月名「晨伏」 ,上三星非晨伏。 夕見者,星比太陽行疾,過合而先行,故夕見,亦曰「西見。」 惟「金、水」 二星及月名「夕見」 ,上三星非夕見。 「晨見」者,星比太陽行遲,合後太陽,故晨見,亦名「東見。」如土、木、火三星及金水逆行,合太陽之後,或初見,或初不見之限。 《同升》者,是二星同過子午線,或同出地平,或同入地平。 《七政遲疾二行論》 日月有遲有疾,五星有遲疾,兼有順逆。星之逆行有限,遲行無限,蓋遲則不行而留。今須求疾遲逆,一日之行若干,始可考其凌犯之自也。 疾者何?視行勝平行,謂之疾;平行勝視行,謂之遲。逆行實不能言疾,蓋退未進之行也。 太陽及諸政之行,在本天最高極遲,在其衝極疾。何者?凡物遠見小,近見大,如太陽一日平行一度,此一度近於人目,則見大,遠則小。大小之分,在人目之視角或天上所掩之分,弧大則近,小則遠。太陽近則視行多,遠則視行少。遠者最高也,近者最庳也。 太陽疾行為六十一分二十秒,遲行為五十七分,太陰疾行為十五度十七分九秒,遲行為十一度一十九分四十九秒二十三微。 土星順疾為八分九秒,逆疾五分十三秒。 木星順疾為十四分二十四秒,逆疾七分四十四秒。 火星順疾四十七分二秒,逆遲三十五分十一秒。 金星順疾一度十六分,逆遲三十八分。 木星順疾,一度五十四分。逆疾一度〇五分。 《五緯天各距地》 求月距地之高,其法有五。又求太陽距地,其法有三:皆以地半徑為度。又各法因高差。〈亦名視差地半徑差等〉或「《日月交食》為本。」 「測恆星之遠」,借用五星之測略定土星之高,并亦得恆星在上之高。今因五緯無視差 土、木二星甚遠,其視差不過數秒。如無差難測,水星常在《蒙》氣中,亦不能測。火、金或有視差,然不足為測其高之本,說見下。 欲測其高,法有二算,或用古圖,或新圖,各有本輪如左: 五緯天距地圖 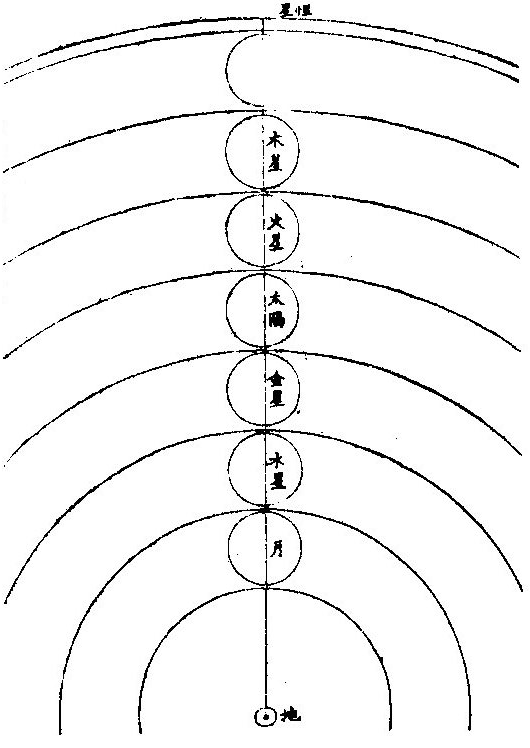 五緯天距地圖說 右《古圖》以地為日月五星恆星,諸天之心,設諸曜,各居一層,天其厚,內函有小輪。〈亦名歲輪〉各層相切而無空,又各層上下有兩面,下內為凹,上外為凸。 各天之厚,因函小輪,其小輪于地有近有遠,如兩心差之理,則各天之厚,為小輪全徑及兩心差之倍分數。 謂分數者,蓋各有均圈,于最高減距高去兩心差之幾分。 圖上各天小輪比本天許小,以指外有兩心差數,本《曆測》各星小輸及兩心差定本天半徑皆為十萬分。若加小輪半徑及兩心差數,必得其最高距地若干。若減之,則得最卑距地若干。如圖。 凡設一層天上面距地若干度?〈以地半徑為一度〉必得其次層下面距地之若干度。蓋兩面中無空隙,又設內面所距若干度,及次層上下兩面距本心比例,以三率法求之,並可得其厚距地之度。法曰:依內面距本心多寡分數,得度多寡,則上距分之某數,必亦可知其度。 月離設三家之數以測定其距地之度,今所為《第谷法》曰:「太陰大距地為六十地半徑有六十分之三十六或百分之六十。」 水星天兩心差為六八二二。〈十萬分為全本天半徑下同〉小輪半徑為三、八、五〇〇兩數並之。 《水星均》圈法:「凡在最高,不減其距地。」 又加半徑。〈全數〉得一四五三二二,乃水星最大距之數。 又前兩數相并,于全數內減之,得五四六七八,乃極近之數也。置極近數為六十度有六十分之三十六,乃月天極高數也。以此度數或約為五分之三,乘極高之數,以小距數除之,得一六一,乃水星天上面距地之度也。 金星在水星上,則其下面距地為一六一。〈奇零不算〉設金星兩心差,為三二〇八,用其半;因有均圈,用其半。他星倣此。為一六〇四。小輪半徑為七二二四八。兩數并加于全數,得大距數為一七三八五二。又兩數相并減于全數,得二六一四八,為近距之數。法以丙面距度之數乘大距數,以近距數除之,得一〇七一,乃金星外面距地之度數也。 太陽有本法求其中距地,得一一四十二地半徑。諸家小異。以求大距,或用均圈,或不用均圈,兩法略差,今不用,只因太陽兩心差求之,得近距為一一〇一,遠距為一一八二。 問:「太陽天內面切金星外而是也。今因太陽本,算其內面盈金星外面三十度,兩算不合,何也?」曰:「此測難求其密。其較雖盈三十度,以全數計之,不及百分之三,數則小矣。」又曰:「所測定各天之數,皆以日月星諸體之心為測,其體之厚,未嘗入數,必月及水、星、金星各數大略,而後算始無差。」又曰:「所用之數,乃新圖之」數,不謂各曜各麗一天而相切,故其數于此論不合。 或曰:「星體到本天最高在此,其天或仍厚幾許,要未可知。」所定之數,亦其大略而已。 火星兩心差為一九六〇取五分之三。 均圈心距地心為三分,不同心圈心距地心五分。 為一一七六〇小輪極大半徑。〈有盈有縮故用大數〉為六五八〇〇。兩數并之,加于全數,得遠大距,為一七七五六〇。兩數并之,減于全數,得近小距,為二二四四〇。用法以太陽大距數一一八二乘火星遠大距數,以近距除之,得九三五二。乃火星外面距地之度數,或木星天內面距地之數也。 木星兩心差為九一六〇。用其半,得四五八〇;小輪半徑為一九二九四。兩數并加全數,得一二三八七四,乃木星遠大距數;兩數并減于全數,得小距數為七六一二六。依前法以內面乘大距,以小距數除之,得一五二一七,乃木星上面距地之數,或土星下面距地之度數也。 土星兩心差為一一六二八,用其半,得五八一四;小輪心半徑為一〇四二六,兩數并加于全數,得一一六二四〇,乃土星大距數也。若以前兩數并減于全數,得小距數為八三七六〇,依前法乘除,得二一一一七,乃土星上面距地之數,或恆星天距地之數也。 右算皆用古圖,以明今測之數。然亞耳《罷德》于《唐僖宗廣明》右算,得水星本天中距地為一百一十五度,金星中距為六百一十八度,火星中距為四千五百八十四度,木星中距一萬〇千四百二十三度,土星中距為一萬五千八百度,恆星中距為一萬九千度。 因各星矩地及其體之視徑,亦并可推其大小。 《用新圖算各星距地》 《新圖》以地為太陽、太陰恆星所行之心;別「五緯」,以太陽為本行之心。又土、木、火三星,以太陽所行之圈為古法。所謂「年歲圈」,即上所用法;今非其真,因用本法。 又《新圖》不言各星各有一天,而強星在本重之內;但各所行之輪,或相切、或相割耳。 各星天距地圖 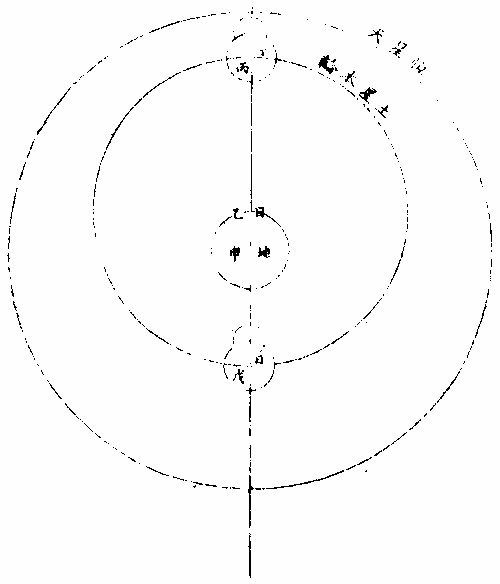 各星天距地圖說 土、木火三星,以太陽為本行之心,又因其心從太陽,即以太陽所行之輪為人目所見每年各星之行。 欲知小輪于本天及兩心差各數比例,則設太陽距地若干,可得各星距地若干。如圖設《甲乙》。〈目距地或小輪半徑〉乙、丙〈星本天半徑為全數〉及丙丁,〈兩心之差〉又設甲乙為若干度,依法可得乙丙丙丁各線之度,并之得甲丁,乃星距地之度也。上三星之法無二,今置土星各圈之數,如土用三率,法甲乙。〈小輪半徑〉為一〇四二六,得距地為一千一百四十二度。〈太陽中距度〉今乙丙全數:〈本天半徑〉得若干算,得一〇九五三有奇。又丙丁五八一四。〈兩心半差〉得六三六。以甲乙乙丙丙丁三線之數并之,得一二九三二度,或地半徑,乃土星大距地之數也。若干乙丙全數,或乙戊半徑數,丙減去甲乙及戊己。〈與丙丁等〉一七七八得九一七五,乃土星近距數,若求其中距地。〈引數為三宮九宮〉得「一〇」,「五」「五〇。」 木星用法如上,求得大距度數為六一九〇,中距:為三九九〇,近距為五九一九。 《火星用法》求得大距為二九九八;中距為一七四五;近距為二二二 金水二星距地圖  《金、水二星距地圖說》 金、水二星,因不圍地球,其算法與上三星略不等。如圖甲乙為日距之線或小輪心距地之線,乙丙為小輪之半徑。以乙甲加減,得大小兩距之數。 金星兩心差:半之,得一六〇四,並加小輪半徑,得一七三八五二。用法《乙甲》全數。〈本天半徑〉得距地二四二度。 今算乙丙分數,得度為八四三,以加于甲丙,得一九八五,乃金星距地之度數也。若減之得三百度,乃近距之度也。 雜論七政及恆星距地說 水星以法求之,得大距度為一六五九,小距為六二五度。 以上因其度數,可推各距地之里數。蓋以地半徑為度,有一度之里數,因可得各距之里數。置地半徑為二萬八千六百六十二里,以各星距地之度乘之,先用古圖數。 月距地小數為六十萬七千六百四十六里有奇,《大距數》為八十六萬七千里有奇,此今古小異。 水星小距數與《太陰》大距數等,其大距數為四百六十一萬二千三百二十八里。 《金星大距數》為三千〇六十七萬二千〇〇八里,《太陽中距》為三千二百七十一萬六千〇一十六里,《大距》為二千三百八十六萬一千九百三十六里,《火星大距數》為二萬六千七百九十一萬六千〇九十六里。 木星大距數為四萬三千五百八十五萬六千六百一十六里。 土星大距數為六萬〇四百九十五萬九千八百一十六里。 恆星依法切土星上面,則得其距地之數。 若用《新圖》推算,亦可得各星之里數。 五星視差圖 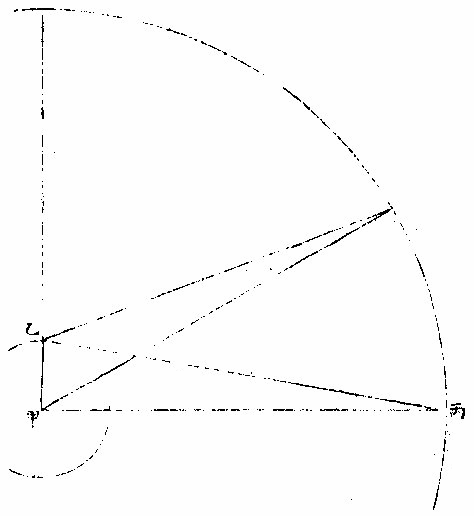 《五星視差圖說》。〈通半徑差。〉 各星既有距地之度數,則可以視差之分數,借日躔《視差圖》以明之。甲地心,乙人目,內為某星,甲乙為一度,若知甲丙邊之度,則可得乙丙甲角乃視差角也。 甲丙當全數,甲乙為切線。 依《古圖》,得各星視差如左: 設星在地平,求其視差,地平以上,若星更高,其差更小;在頂,無。 月近地視差。 《水星距遠視》差為二十一分。 《金星距遠視差》與太陽距近差數等,為三分七秒,太陽中距為三分,大距為二分五十四秒。 火木土三星,其視差皆不滿一分,故不算。 「若用《新圖》」,日月各視差無二。 金、水二星中距與太陽為近,金星距遠視差為二分,弱極近距為十一分,水星大距亦為二分,小距為六分。 上三星之差亦微,但火星在極近之距即太陽之衝,其差為十五分。蓋其道切割太陽之道,而于地更近。 以上視差之數,日月以外,難測難定,是以各家不合,且不常用,故不設表。 《五星體視實兩徑》 測日月視徑實徑見《月離》及《交食》諸書皆有本論,但日月體大,可用儀器測定;五緯體小,測之為難。惟以人目所見,或于日月相比以定其視徑,後以近遠之數求其實徑、大小相比等數。 亞耳巴得其學本多祿某有曰:「水星中距地之時{{Annotation|,本算得一百一十五度,}}其視徑比太陽視徑如十五分之一,即天度。」〈周天三百六十度之度也〉之二分《金星中距時》。〈本算為六百一十八度〉其視徑,為太陽視徑十分之一,即天度之三分火星中距。〈本算為四千五百八十四度〉其視徑為太陽視徑二十分之一,即天度之分半木星中距。〈本算為一萬〇四百二十三度〉其視徑,為太陽視徑十二分之一,即天度之二分半,土星中距。 〈本算為一萬五千八百〇〇度〉其視徑為太陽視徑十八分之一,即天度之一分四十三秒。 五星視實兩徑圖  《五星視實兩徑圖說》: 又「星高有視徑」,以法求實,徑如圖甲人目。〈地心無異〉「乙庚太陽半視徑,乙己某星半視徑」,其比例如乙己于乙庚,若星在太陽如丙丁,則其比例為丙丁與丙戊。〈丙戊當太陽視徑〉用法得丙丁天上度之幾分。有丙丁分數,則有本天周之分數。因周與徑之比例,甲丙半徑得地半徑若干,則其周得若干。以周之某分若干,得各星比例半徑大小。又以各星同類之分數求其容。 依法算,得水星體比地球小,為一萬一千分之一分。 金星體小于地球為三十六分之一分。 火星體大,為一地球又三分之一; 木星體比地球大,為八十一倍,又曰「九十五倍」;土星體大于地球,為七十九倍,又曰「九十一倍。」用《新圖》求各星大小。 《新圖》以太陽為五星之心,金、水二星,或在日上,或在日下,與古法大異。 《第谷》曰:「水星視徑中距時。」〈一一五〇度〉為二分〇十秒,其實徑與地徑為三與八,則其體小於地球,為十九分之一,于古法甚遠。《金星視徑》中距時,〈一一五〇度〉為三十三分十五秒,其實徑為地球徑十一分之六,則其容為地球六分之一。《火星中距》:〈一七四五度〉「視徑」為二分弱,則其實徑為地徑六十分之二十五強,其體小于地球,為十三分之一弱。《木星中距》:〈三九九〇度〉視徑為二分四十五秒,其實徑于地為十二與五,則其體大于地球,為十四倍。土星中距:〈一〇五五〇度〉「視徑」為一分五十秒,其實徑為二。地球徑又十分之一,則其體大于地球為二十二倍。 若欲以里數求各星之大,則先求地球之容得里數,次依各比例數求之。 問:「古今兩數相懸,何者為確?」曰:「各有本論,然以金星證之,見其繞太陽,亦有弦朢之異,覺新法為準。」 《五星光色》 「月以光以魄,知其光非本體之光,乃所借于太陽之光。金星亦然。蓋以遠鏡窺之,見其體亦如月,有光有魄故也。他星覺無所倚。然以相似之理論之,亦可謂其光非自光,乃如月與金星並借光于太陽者也。」問:「五緯之光既皆為日光之分,乃其色各不同者,何也?」曰:「如鏡、如水、如金諸能發光之物,咸受太陽之光,而」所發之光,皆非一色。蓋亦繇「本體之色」所染故也。 然則五星之色,亦各為本體之色,從日光而發見耳。 五星本體之色,從其各類本質及其面之平與不平,或其體之虛實堅脆等勢所發。 《加利婁》曰:「凡大光照某體能發光之類,其所發之次光,非全受本體之色而變為他色,如大光照黑體。」〈若煉鐵〉其所發之光為「紅色」如火星。〈以此西名火星亦謂之鐵星〉若照《淡紅體》,其所發光,色如木星。〈紅銅色為淡紅故木星亦名為銅星〉「若白體,其發光色如土星。若黃體,其發光色如金星。若青體,其發光色如水星。」試以黑鐵等類煉之,細閱其光色必如上。 又曰:「星色非純,從目審視可見,乃知各星亦非純質也。」 「五星時有顫動,其理與恆星無異,或空中浮氣之游移,或自體閃爍如燭光之搖,又或人目之缺。 |
| 梦远书城(guxuo.com) |
| 上一页 回目录 回首页 下一页 |